مقالات آمار و احتمال
یادآوری احتمال
Table of Contents
پدیده (Event):
علم آمار و احتمال با نگاه عمیق و موشکافانه به مطالعه پدیدههای پیرامون میپردازد. پدیدههایی که در دنیای واقعی با آنها مواجه هستیم دو حالت دارند:
- قطعی: مثل قوانین فیزیکی، اصول طبیعت مانند مرگ
- غیرقطعی: مثل پرتاب تاس، سکه، وضعیت آب و هوا
اکثر پدیدههایی که در دنیای واقعی با آنها سر و کار داریم پدیدههای غیرقطعی هستند.
تفکیک انواع پدیدهها از این منظر و تشخیص حالات متصور برای آنها جهت بررسی و شناخت نوع آنها حائز اهمیت میباشد.
آزمایش تصادفی:
آزمایشی که نتیجهی نهایی آن پیش از آزمایش قابل تعیین نمیباشد اما تمام نتایج ممکن آن مشخص میباشند.
فضای نمونه:
تمام نتایج ممکن و قابل تصور از آزمایش تصادفی
مثال، در پرتاب دو تاس، فضای نمونه به چه شکل است؟
مساله میتواند از دو منظر تمایز یا عدم تمایز میان دو تاس بررسی شود.
اگر تاسها متمایز باشند، ۳۶ حالت خواهیم داشت.
اگر تاسها متمایز نباشند، باید زوجهای تکراری را یک بار در نظر گرفت، زیرا ۳۰ زوج تکراری داریم که در مجموع با ۶ زوج تکرار نشدهی (۱،۱) ، (۲،۲) ، (۳،۳) ، (۴،۴) ، (۵،۵) و (۶،۶) مجموعا ۲۱ حالت خواهیم داشت.
مثال، فضای نمونه در یک مسابقه فوتبال را بررسی کنید.
این مساله میتواند از نگاههای مختلفی بررسی شود.
از نظر نتیجه: { برد تیم اول، تساوی، برد تیم دوم }
از نظر گلهای بازی: {۰, ۱, ۲, ۳, ۴, …} = اعداد صحیح نامنفی
از نظر تعداد گلهای هر تیم: زوجی از تعداد گل تیم اول و تعداد گل تیم دوم (اعداد صحیح نامنفی، اعداد صحیح نامنفی)
از نظر تعداد کارت اخطار: زوجی از تعداد کارت زرد و تعداد کارت قرمز (اعداد صحیح نامنفی، اعداد صحیح نامنفی)
از نظر پایان مسابقه: {۹۰ دقیقه، ۱۲۰ دقیقه، پنالتیها}
بنابراین میتوان به یک پدیده را از حالتهای فراوان و متنوعی نگاه کرد.
پیشامد:
هر زیرمجموعهای از فضای نمونه
تعداد کل پیشامدهای ممکن: ۲n(S)
پیشامد توصیفی: بیان مفهومی، مانند اعداد زوج در پرتاب تاس، گل زدن تیم یک
شمارشی: بیان دقیق و بصورت شمارش شده
مثال، در مسابقهای از لیگ برتر فوتبال، فضای نمونهی امتیازات دو تیم از مسابقه و یک نمونه پیشامد از آن را بیان کنید.
فضای نمونه بصورت زوج مرتبی از امتیاز کسب شده هر تیم: {(۰, ۳), (۳, ۰), (۱, ۱)}
نمونه پیشامد: بصورت توصیفی، امتیاز گرفتن هر دو تیم بصورت شمارشی، (۱, ۱)}}
متغیر تصادفی:
تابعی که به هر یک از اعضای فضای نمونه، عددی حقیقی نسبت میدهد.
![]()
از آنجا که پدیده تصادفی است، متغیر تصادفی که نگاشتی از فضای نمونهی پدیده میباشد نیز تصادفی خواهد بود.
یک متغیر تصادفی مانند توابع دیگر، شامل دامنه و برد میباشد.
دامنه: اعضای فضای نمونه
برد: زیر مجموعهای از اعداد حقیقی متغیر تصادفی
مثال: در پرتاب تاس نمونهای از متغیر تصادفی تعریف کنید.
متغیر تصادفی تابع همانی: f(x)=x
دامنه: فضای نمونه = {۱, ۲, ۳, ۴, ۵, ۶}
برد: {۱, ۲, ۳, ۴, ۵, ۶}
مجموع اعداد حاصل از پرتاب دو تاس: f(x,y)=x+y
دامنه: {(۱, ۱), (۱, ۲), (۱, ۳), …, (۶, ۴), (۶, ۵), (۶, ۶)}
برد: {۲, ۳, ۴, ۵, ۶, ۷, ۸, ۹, ۱۰, ۱۱, ۱۲}
احتمال:
فراوانی رخداد پیشامدی از فضای نمونه در تکرار بیشمار آزمایش تصادفی.

مفهوم احتمال بر اساس دادهها و تجارب گذشته است. در مسائل روزمره، نقش گذشته در احتمال برجسته است. برای نمونه در بررسی احتمال اینکه نرخ تورم سال آینده دو رقمی باشد، میتوان به نرخ تورم در سالیان گذشته رجوع و بر اساس آن، دیدگاه ارائه کرد.
در راستای قوی تر شدن این دیدگاه میتوان:
- تعداد نمونهها را افزایش داد، به عبارتی در مثال بالا، سالیان بیشتری را در نظر گرفت.
- نمونههای مشابه با شرایط فعلی را در نظر گرفت، به عبارتی در مثال بالا، سالیان تحریم را در نظر گرفت.
بطور کلی با افزایش اطلاعات درباره پدیده، دامنه خطا کاهش پیدا میکند و دیدگاه دقیق تر میشود.
توابع مهم:
تابع چگالی احتمال (Probability Distribution Function):
احتمال رخداد پیشامد به ازای آن پیشامد تعریف میشود.
تابع جرم احتمال (Probability Mass Function):
مانند تابع چگالی احتمال اما برای متغیر تصادفی های گسسته بکار میرود.
تابع توزیع تجمعی (Cumulative Distribution Function):
مجموع احتمالات تا پیشامدی مشخص یا احتمال رخداد مقادیری که کمتر یا برابر مقداری مشخص هستند. (مساحت)

امید ریاضی (Expected value):
میانگین وزنی متغیر تصادفی که ضرایب وزنی، احتمال رخداد هر مقدار هستند.
به عبارتی دیگر: مرکز ثقل احتمالات؛ میانگین مقادیر حاصل از انجام بیشمار مرتبه آزمایش تصادفی
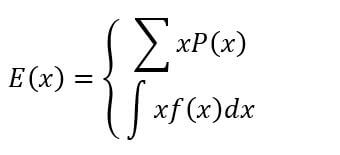
تصور اشتباه از امید ریاضی: مقداری که احتمال رخداد آن از بقیه بیشتر است.
گشتاور (Moment):
امید ریاضی متغیر تصادفی حول یک نقطه با مرتبهای مشخص.
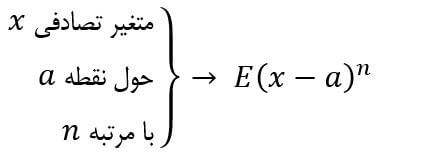
حالتهای خاص گشتاور:
- امید ریاضی: گشتاور مرتبه اول حول مبدأ:

- واریانس: گشتاور مرتبه دوم حول میانگین:

قضیه محورهای موازی:
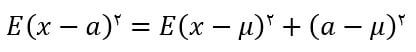
نتایج:
واریانس حد پایین گشتاورهای مرتبه دوم یک متغیر تصادفی میباشد.
به عبارتی در میان تمام گشتاورهای مرتبه دوم یک متغیر تصادفی، واریانس دارای کمترین مقدار است.
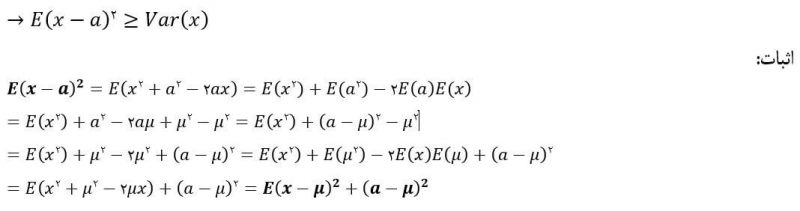
رابطهای میان واریانس و امید ریاضی:
![]()
احتمال شرطی:
کوچک کردن فضای نمونه با اضافه کردن اطلاعات جدید.
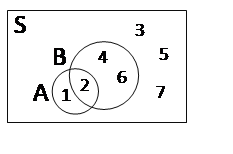
شکل مقابل فضای نمونهی اولیهی پرتاب یک تاس است که A عبارت است از کمتر از ۳ آمدن تاس و پیشامد مورد بررسی میباشد. اگر B که بیانگر زوج آمدن تاس میباشد به دانستههای پدیده اضافه شود، A∩B و B به ترتیب پیشامد و فضای نمونهی جدید ما با توجه به اطلاعات جدید خواهند بود که نسبت به قبل کوچکتر شدهاند.
استقلال:
بی تاثیر بودن وقوع یا عدم وقوع پیشامدی بر پیشامد دیگر
![]()
توجه: تهی بودن اشتراک دو پیشامد نشانگر استقلال نیست، بلکه بیانگر ناسازگاری دو پیشامد است.
مفهوم استقلال به این اشاره دارد که دانستن یا ندانستن از یک موضوع تاثیری در احتمال رخداد مورد بررسی نداشته باشد. برای مثال در پرتاب همزمان سکه و تاس، آگاهی از نتیجهی پرتاب سکه، تاثیری بر نتیجهی حاصل از پرتاب تاس ندارد.
مثال:
در پرتاب یک تاس داریم:
A= {1,2,3} B ={1,3,5} C ={2,4,6}
{۱,۳,۵}= E= {1,2} F
مطلوب است محاسبه
- P(A|B)
- P(A|C)
- P(E|F)
و تعیین کردن استقلال دو پیشامد.
پاسخ:
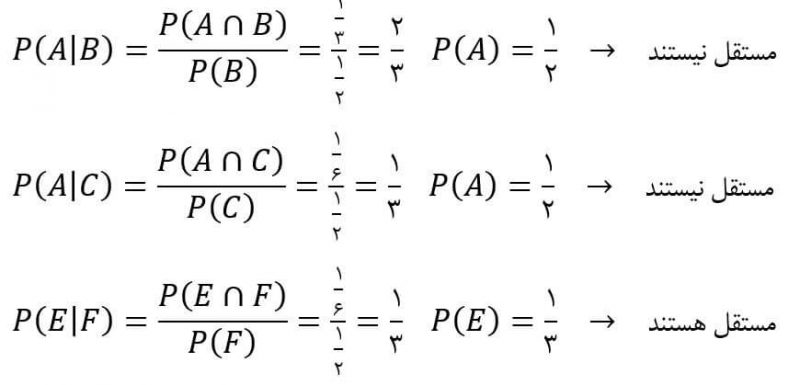
نمونه گیری (Sampling):
نمونه گیری اولین موردی است که در آمار مطرح میشود. غالبا بررسی کل جامعه به راحتی امکان پذیر نیست، زیرا نیازمند پرداخت هزینه و زمان زیادی میباشد. از همین جهت نمونه گیری مورد توجه قرار میگیرد، هرچند از دقت کامل برخوردار نیست، اما در حد خوبی نیازهای مطالعه را برآورده میکند. نمونه گیری باید تصادفی باشد.
مثال، در نمونهگیری از مدت زمان معطل شدن مراجعان به پلیس +۱۰:
جامعه کل مراجعات به پلیس +۱۰ است.
نمونه تصادفی مراجعه تصادفی در مکانها و زمانهای مختلف به پلیس +۱۰ و ثبت نمونهها به شکلی که استثناء نباشند.
نمونه تصادفی(IID):
متغیرهای تصادفی با دو ویژگی زیر نمونه تصادفی تشکیل میدهند.
- از یکدیگر مستقل باشند. Independent
- از نظر نوع و پارامترهای توزیع مشابه باشند. Identical Distribution
توزیع نرمال و نرمال استاندارد:
پرکاربردترین توزیع احتمالی پیوسته میباشد که در آن دادهها پیرامون مقداری ثابت (میانگین)، پراکنده (واریانس) شدهاند.
بسیاری از پدیدههای طبیعی و فیزیکی از این توزیع پیروی میکنند. این توزیع دارای شکلی زنگوله مانند است که حول میانگین متقارن است.
این توزیع دارای دو پارامتر میانگین و واریانس است.
در حالت خاص، اگر میانگین و واریانس به ترتیب برابر ۰ و ۱ باشند، توزیع نرمال استاندارد نامیده میشود.
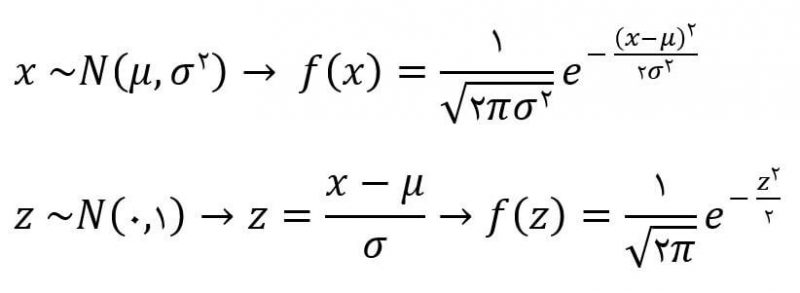
در محاسبه سطح زیر نمودار نرمال، ابتدا توزیع را استاندارد کرده و سپس از جدول نرمال استاندارد استفاده میکنیم.
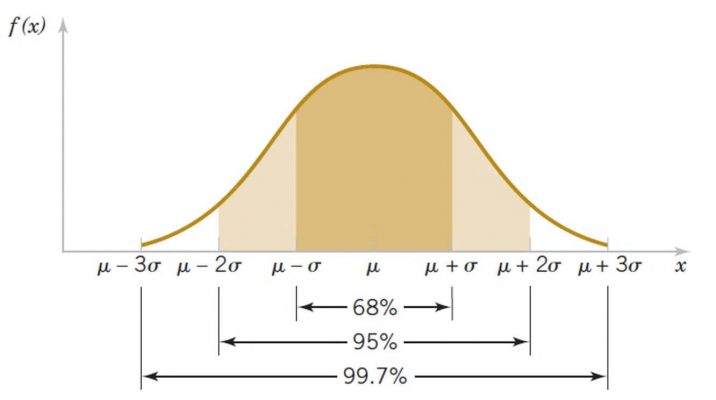
![]()
![]()
![]()
ترکیب خطی متغیرهای تصادفی:
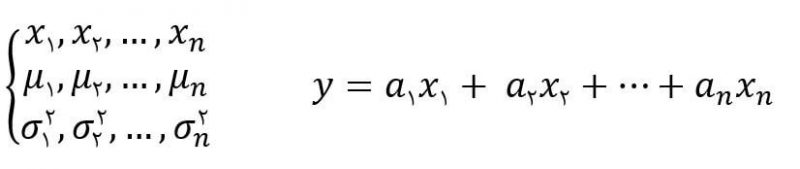
مستقل بودن متغیرهای تصادفی در محاسبه امید ریاضی تاثیری ندارد. بنابراین در حالت کلی و همیشه برقرار:
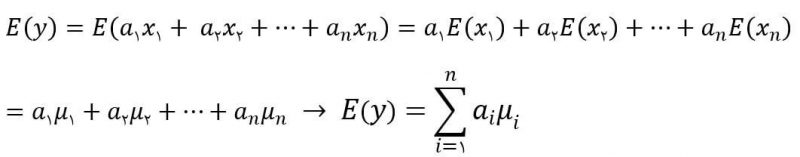
مستقل بودن متغیرهای تصادفی در محاسبه واریانس تاثیرگذار است. بنابراین با فرض مستقل بودن متغیرهای تصادفی یعنی صفر بودن کوواریانس:
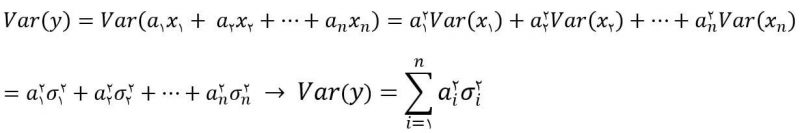
حالات خاص ترکیب خطی متغیرهای تصادفی
- متغیرهای تصادفی مستقل با یک نوع توزیع:
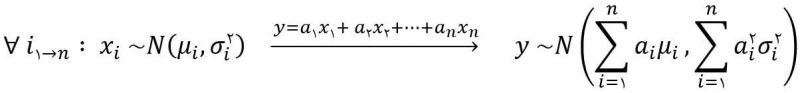
در این حالت مقادیر میانگین و واریانس تفاوتی با حالت کلی ندارند اما علاوه بر آن y نیز از توزیع نرمال پیروی خواهد کرد.
- متغیرهای تصادفی مستقل با یک نوع توزیع و پارامتر، یعنی نمونه تصادفی (IID):
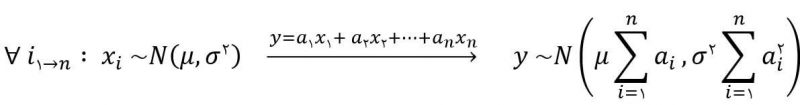
- نمونه تصادفی نرمال با ضرایب برابر یک:
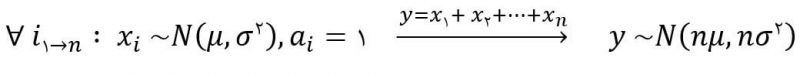
- میانگین نمونه:
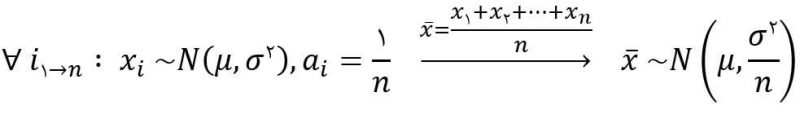
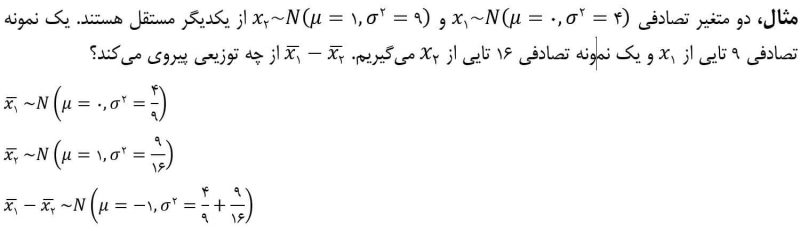
تا اینجا میدانیم که ترکیب خطی دستهای از متغیرهای نرمال از توزیع نرمال پیروی میکند. اما در صورتی که متغیرهایی با توزیع غیر نرمال مورد بررسی قرار بگیرند ترکیب خطی آنها از چه توزیعی پیروی خواهد کرد؟ اینجاست که قضیه حد مرکزی به عنوان یک شاهکار مطرح میشود.
قضیه حد مرکزی:
میانگین ( یا مجموع ) n متغیر تصادفی X۱ , X۲ , … , Xn هنگامی که n به سمت بینهایت میل میکند فارغ از نوع توزیع و پارامتر، از توزیع نرمال پیروی خواهد کرد.
به عبارتی، مهم نیست که متغیرهای تصادفی از توزیع نرمال پیروی کنند یا خیر، هر چه تعداد این متغیرهای تصادفی از هر توزیعی بیشتر شود، رفتار میانگین (یا مجموع) آنها بیشتر به توزیع نرمال نزدیک میشود.
در صورتی که n>=25 باشد حد مرکزی کاربرد پیدا میکند.
فیلم آموزشی
سوالات حل شده در کلاس حل تمرین
سوالات تکلیف مربوط به توزیع نرمال
برای دانلود جدول توزیع نرمال روی نوشته زیر کلیک کنید.
