برآورد نقطه‌ای (Point Estimation)

استنتاج آماری(Statistical Inference):

تصمیم گیری و نتیجه گیری درباره جامعه‌ها با استفاده از روش‌های آماری را استنتاج آماری می‌نامند. در این روش‌های آماری، از اطلاعات موجود درباره نمونه برای تصمیم گیری استفاده می‌شود. استنتاج آماری به دو زمینه‌ی برآورد پارامتر و آزمون فرض تقسیم می‌شود. برای مثال، در برآورد پارامتر، مهندسی به دنبال تخمین بازدهی یک فرایند در دو دمای مشخص است. اما در آزمون فرض، او به دنبال این است که نشان دهد فرایند در دمای دوم، بازدهی بهتری نسبت به دمای اول دارد.

برآورد پارامتری دارای دو نوع برآورد نقطه‌ای و برآورد فاصله‌ای می‌باشد.

استنتاج آماری همواره بر نتیجه گیری در مورد یک یا چند پارامتر از جامعه متمرکز است. یکی از بخش‌های مهم این فرآیند، برآورد پارامترها است. همانطور که قبل‌تر آشنا شدیم، در برآورد با استفاده از دانسته‌ها که همان اطلاعات بدست آمده از نمونه هستند، درباره چیزهایی که نمی‌دانیم، یعنی اطلاعات توزیع و جامعه اظهار نظر می‌کنیم.

برآورد نقطه‌ای، نگاشتی از اطلاعات نمونه به یک نقطه مشخص می‌باشد. به عبارتی، با استفاده از داده‌های نمونه، تلاش می‌شود تا به یک مقدار معقول که ذهنیتی از پارامتر مجهول می‌باشد دست یافت. تا اینجا ما با این نوع برآوردگر کار می‌کردیم. برای مثال وقتی میانگین یک جامعه را ۵.۶ تخمین بزنیم، برآوردی نقطه‌ای انجام داد‌ه‌ایم.

آماره (Statistic):

به هر تابع و نگاشت از مشاهدات آماره می‌گویند. بنابراین هر مشاهده (بصورت تابع همانی) یا هر برآوردگر نقطه‌ای نیز در حقیقت یک آماره است. آماره بر اساس اطلاعات نمونه می‌باشد بنابراین شامل پارامترهای مجهول و غیرقابل محاسبه نیست و باید پس از نمونه گیری، قابل محاسبه باشد. از آنجا که آماره متغیری تصادفی می‌باشد، دارای توزیع احتمالی است که توزیع نمونه نامیده می‌شود. توزیع نمونه به توزیع جامعه، اندازه نمونه و روش نمونه گیری بستگی دارد. مهمترین این توزیع‌ها نرمال است که در شرایط مجهول بودن توزیع جامعه نیز، بر اساس قضیه حد مرکزی، توزیع نمونه را بصورت تقریبی نرمال در نظر می‌گیریم.

در نهایت، هدف از برآورد نقطه‌ای، انتخاب یک عدد واحد بر اساس داده‌های نمونه است که قابل قبول ترین مقدار برای θ باشد.برآورد در مهندسی به شدت مورد نیاز است و غالبا به برآوردهای زیر نیاز داریم.

ممکن است چندین انتخاب متفاوت برای برآوردگر نقطه‌ای یک پارامتر داشته باشیم. به عنوان مثال، اگر بخواهیم میانگین یک جامعه را تخمین بزنیم، ممکن است میانگین نمونه، میانه نمونه یا شاید میانگین کوچکترین و بزرگترین مشاهدات در نمونه را به عنوان برآوردگر نقطه‌ای در نظر بگیریم. برای اینکه تصمیم بگیریم کدام برآورد‌گر نقطه‌ای از یک پارامتر خاص بهترین است، باید ویژگی‌های آماری آن‌ها را بررسی کنیم و معیارهایی را برای مقایسه برآوردگرها ایجاد کنیم.

برآوردگر نقطه‌ای بهینه:

نااریب بودن و کمینه بودن واریانس شاخصه‌های اصلی یک برآوردگر مناسب هستند.

با ویژگی نااریب بودن آشنا شدیم. نااریب بودن به نوعی عبارت است از نزدیک بودن برآوردگر به مجهول که به بیان رسمی، اگر مقدار مورد انتظار برآوردگر برابر با مجهول باشد، برآوردگر نااریب خواهد بود. اما منظور از کمینه بودن واریانس چیست؟ مفهوم واریانس تداعی کننده پراکندگی و فاصله از میانگین است. بنابراین هنگامی که واریانس کمتر باشد، مقادیر برآوردگر به میانگین برآوردگر نزدیک تر می‌شود که در صورت نااریب بودن، این به معنی نزدیک تر شدن برآوردگر به خود مجهول است.

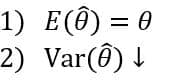
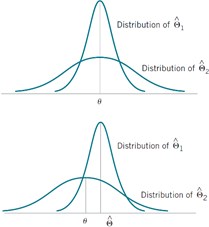
مفهوم واریانس یا گشتاور مرتبه دوم حول میانگین، تداعی کننده فاصله از میانگین است. بنابراین هنگامی که واریانس کمتر باشد، مقادیر برآوردگر θhat به میانگین برآوردگر   (θhat)E نزدیک‌تر می‌شود که در حالت نااریب بودن، این به معنی نزدیک تر شدن برآوردگر به خود مجهول θ است.

مثال: داده‌های مربوط به میزان رسانس گرمایی یک ماده در جریان یک عملیات حرارتی که حاصل از اخذ یک نمونه ۱۰ تایی می‌باشد، به این صورت است:

۴۲/۰۴، ۴۱/۸۱، ۴۲/۲۶، ۴۱/۷۲، ۴۲/۱۸، ۴۱/۸۶، ۴۱/۹۵، ۴۲/۳۴، ۴۱/۴۸، ۴۱/۶

برای میانگین رسانش گرمایی ماده مورد مطالعه یک برآوردگر ارائه کرده و از نگاه معیار MVUE  این برآوردگر را بسنجید.

پاسخ:

مثال: برای نمونه سه تایی x_۱,x_۲,x_۳، کدام برآوردگر مناسب‌تر است؟

پاسخ:

ابتدا شرط نااریب بودن و سپس کمترین واریانس را مورد بررسی قرار می‌دهیم.

میانگین مربعات خطا (Mean Squared Error)

در تخمین یک پارامتر مجهول، نیاز است تا درباره دقت آن برآوردگر اظهار نظر کنیم. تفاوت برآوردگر و مجهول نشان ‌دهنده خطای آن برآورد است. از آنجا که این مقدار خطا می‌تواند مثبت یا منفی باشد برای خنثی نشدن مجموع خطا، آن را به توان دو می‌رسانیم. اگر از قدر مطلق استفاده می‌کردیم، در مشتق گرفتن دچار مشکل می‌شدیم.

Squared Error:  (θhat – θ)^۲

اما از سوی دیگر، پارامتر مجهول θ قابل بدست آوردن نیست. بنابراین به سراغ امید ریاضی می‌رویم.

Mean Squared Error: MSE(θhat)= E(θhat – θ)^۲

نتیجه مهم این رابطه با استفاده از روش پلاتینی و قضیه محورهای موازی به صورت زیر بدست می‌آید.

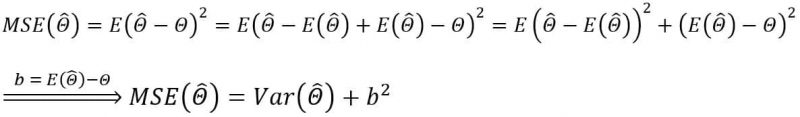
در صورتی که مقدار b برابر صفر باشد به این معناست که برآوردگر نااریب است.

این رابطه، دقت برآوردگر را هم از نگاه میزان اریبی و هم از نگاه واریانس نشان می‌دهد. واضح است که وقتی میزان اریبی صفر باشد، برآوردگر نااریب خواهد بود. لذا MSE اطلاعاتی از دقت انواع برآوردگر اریب یا نااریب را به ما می‌دهد. گاهی ممکن است یک برآوردگر اریب MSE کمتری نسبت به یک برآوردگر نااریب داشته باشد که باید بررسی با توجه به در اولویت بودن برآوردگر نااریب انجام شود.

کارایی نسبی (Relative Efficiency)

معیاری دیگر برای مقایسه دو برآوردگر که با کسری از نسبت میانگین مربعات خطای دو برآوردگر، میزان کارایی برآوردگر مخرج را به برآوردگر صورت ارائه می‌کند.

توجه: کارایی معیاری با جنبه مثبت و خطا معیاری با جنبه منفی است، بنابراین:

برای ارائه برآورد نقطه‌ای روش‌هایی وجود دارد که در ادامه به آنها خواهیم پرداخت.