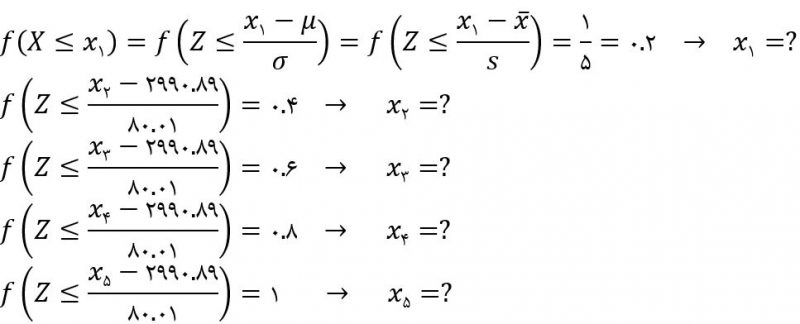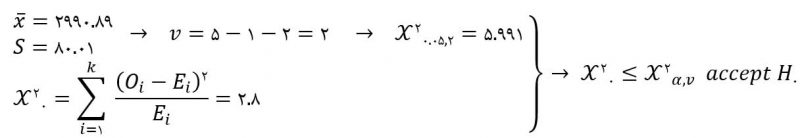آزمون نیکویی برازش (GOF: Goodness of Fitness)

ویدیوی آموزشی

https://aparat.com/v/upxrq

یکی از مشکلات آزمون کولموگروف-اسمیرنف این است که فرضیه شامل پارامترهای توزیع می‌شود، بنابراین اگر فرض صفر رد شود، تنها مشخص می‌شود که داده‌ها از توزیع مفروض با پارامترهای مفروض پیروی نمی‌کنند، اما مشخص نمی‌گردد که آیا داده‌ها از توزیع مفروض، فارغ از مقدار پارامترها پیروی می‌کنند یا خیر. در چنین مسائلی که پارامترهای توزیع می‌توانند مدنظر نباشند، آزمون برازندگی مربع کای مطرح می‌شود. همانند آزمون قبل، مشاهدات شامل n داده با توزیعی نامعلوم هستند.

مراحل آزمون نیکویی برازندگی:

• بازه‌هایی بر اساس توزیع مفروض تشکیل می‌شود که باید شامل شرایط زیر باشند:
  • فراوانی مورد انتظار هر بازه با بازه دیگر یکسان باشد؛ یعنی احتمال قرار گرفتن یک مشاهده در هر یک از فواصل برابر باشد. به عبارتی دیگر، مساحت زیر نمودار بازه‌ها با هم مساوی باشد.        i: E_i=E_i+1∀
  • بازه‌ها به گونه‌ای انتخاب شوند که فراوانی مورد انتظار در هر بازه حداقل ۵ باشد. زیرا فراوانی‌های پایین مستعد خطای زیادی هستند. E_i>=5
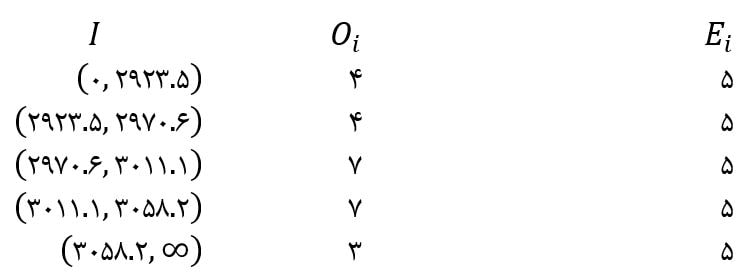
• فراوانی داده‌ها در هریک از بازه‌ها ثبت می‌شود.

• مقدار آماره را بدست می‌آوریم و قضاوت می‌کنیم.

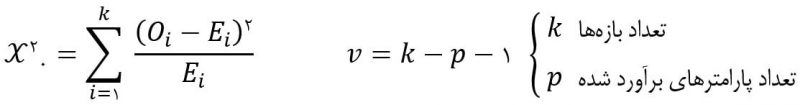
• تصمیم‌گیری (قضاوت)

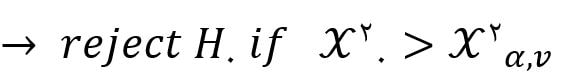
مثال: مثال قبلی را با آزمون نیکویی برازندگی حل کنید. فرض صفر: توزیع نرمال است.

پاسخ: طبق مراحل بالا پیش می‌رویم

۲۵ داده داریم که با توجه به شرایط حداقل فراوانی تعداد مشاهدات، ۵ بازه تشکیل می‌دهیم. x ها انتهای بازه‌ها هستند.