آزمون‌های تعیین شکل توزیع-آزمون کولموگروف-اسمیرنف

ویدوی آموزشی

https://aparat.com/v/4uaxN

منطق این آزمون بر اساس تابع توزیع تجمعی توزیع مفروض است. در این آزمون تابع توزیع تجمعی تجربی که بر اساس داده‌های مشاهده شده تشکیل می‌شود و با تابع توزیع تجمعی توزیع مفروض مقایسه می‌گردد.

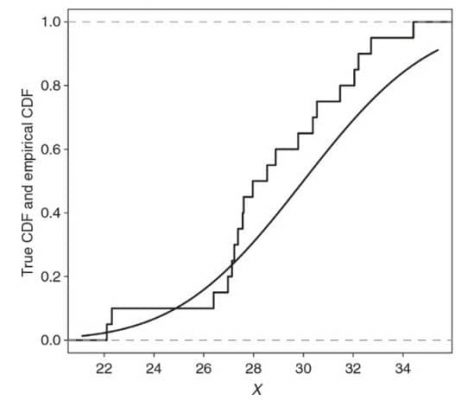
• تابع توزیع تجمعی یک تابع صعودی است. البته اکید نیست.
• تابع توزیع تجمعی مفروض پیوسته است اما تابع توزیع تجمعی تجربی یک تابع گسسته خواهد بود.
• این آزمون هنگامی کاربرد دارد که هم توزیع و هم پارامترهای آن در فرض صفر مشخص شده باشند.
• F(x)=f(x<=X)

برای مثال داده‌های یک آزمایش پرتاب تاس را در نظر بگیرید:

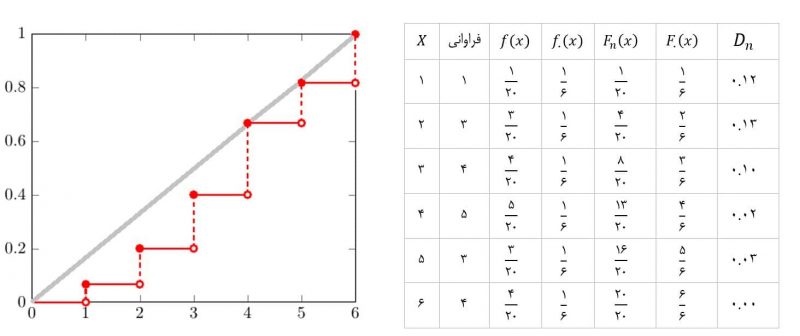
حال برای مقایسه‌ی تابع توزیع تجمعی باید اختلاف و شکاف بین تابع توزیع تجمعی مفروض و تابع توزیع تجمعی رسم شده بررسی شود که در آن بیشینه این تفاضل‌ها انتخاب شده و بصورت زیر آزمون انجام می‌گردد:

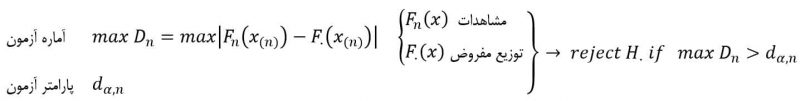
که d_α,n با توجه به جدول زیر بدست می‌آید:

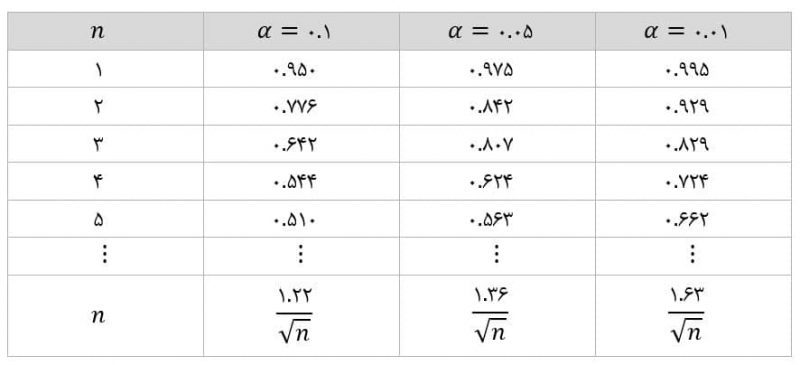
مراحل آزمون کولموگروف-اسمیرنف:

۱- داده‌ها را از کوچک به بزرگ مرتب می‌کنیم.

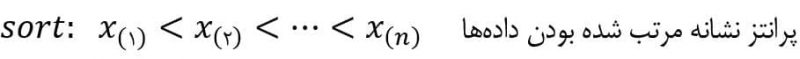
۲- و  تمام داده‌ها را بدست می‌آوریم و در جدول ثبت می‌کنیم.

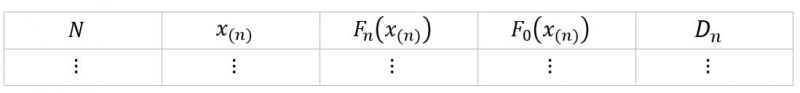
۳- در صورت نیاز نمودار تابع توزیع تجمعی را ترسیم می‌کنیم.

۴- تفاضل‌ها را محاسبه می‌کنیم و در ستون جدول ثبت می‌کنیم.

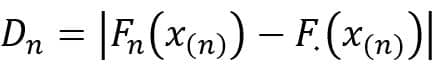
۵- بیشینه تفاضل‌ها را بدست می‌آوریم.

۶- نتیجه‌گیری (قضاوت)

نکته: در بدست آوردن مقدار تابع توزیع تجمعی مفروض از جدول‌ها استفاده می‌کنیم. برای مثال اگر توزیع مفروض نرمال با میانگین ۳۰۰۰ و انحراف معیار ۱۰۰ باشد، برای بدست آوردن مقدار تابع توزیع تجمعی نرمال در نقطه ۳۰۵۳.۰۲ بصورت زیر عمل می‌کنیم:

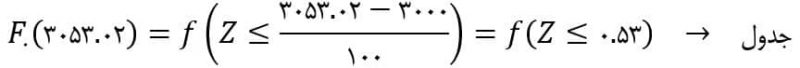
مثال: داده‌های مربوط به مقاومت کششی یک ماده لاستیکی داده شده است. آیا این داده‌ها دارای توزیع نرمال با میانگین ۳۰۰۰ و انحراف معیار ۱۰۰ هستند؟ سطح معناداری را ۵ درصد در نظر بگیرید.

پاسخ: طبق مراحل بالا پیش می‌رویم.

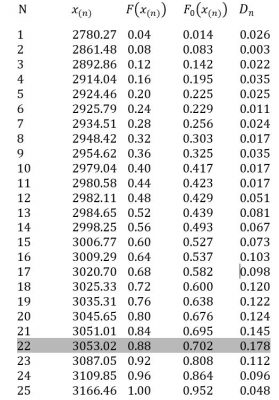
که در نهایت خواهیم داشت:

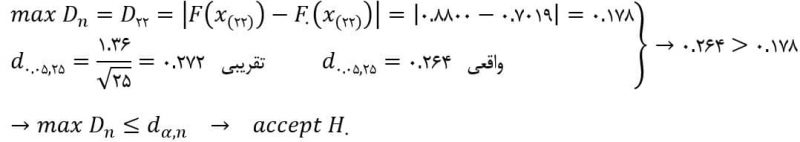
در تفسیر یعنی داده‌ها دارای توزیع نرمال با میانگین ۳۰۰۰ و انحراف معیار ۱۰۰ می‌باشند