قانون بیز در احتمال

مترجم: سید مهدی باغی

ویرایش: ابوالفضل ملکی

قانون بیز

محاسبه احتمال پسین (P(A_j|B از احتمالات پیشین داده شده(P(A_i و احتمال شرطی(P(B|A_i پرکاربرد است. قانون عمومی برای چنین محاسباتی که در واقع تنها یک کاربرد ساده از قانون ضرب است، به توماس بیز فقید برمی‌گردد که در قرن هجدهم زندگی می‌کرد. برای بیان آن ما ابتدا به یک نتیجه دیگر نیاز داریم. به یاد داشته باشید که پیشامدهای  A_۱, …, A_k در صورتی که هیچ جفتی از آنها خروجی و نتیجه مشترکی نداشته باشند(به عبارتی با هم رخ ندهند)، جدا یا ناسازگار نامیده می‌شوند. همچنین این پیشامدها در صورتی که یک A_i الزاما رخ دهد، جامع و کامل بوده و بنابراین S = A1 ∪ … A_k

قانون احتمال کل

فرض کنید A_۱, …, A_k پیشامدهای ناسازگار و جامع هستند. پس برای هر پیشامد دیگر B:

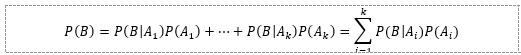
اثبات:

به این دلیل که A_iها ناسازگار و جامع هستند، اگر B اتفاق بیفتد باید دقیقا توام با یکی از  A_iها رخ دهد. این یعنی (B= P(A_۱∩B) ∪…∪ P(A_k∩B ، که در آن پیشامدهای A_i∩B ناسازگار هستند. این تقسیم‌بندی B در شکل زیر تشریح شده است. بنابراین:

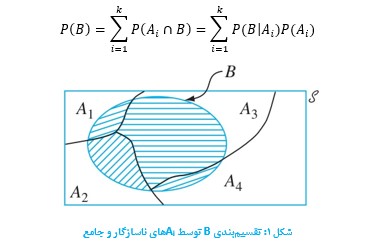
مثال۱:

شخصی سه حساب ایمیل متفاوت دارد. اغلب پیغام‌های او، در واقع ۷۰% پیغام‌های او به حساب #۱ می‌آیند، در حالیکه  ۲۰% به حساب #۲ و ۱۰% باقیمانده به حساب #۳ می‌آیند. از پیغام‌های حساب #۱، تنها ۱% تبلیغ(هرزنامه) هستند در حالیکه درصدهای متناظر برای حساب‌های #۲ و #۳ به ترتیب برابر با ۲% و  ۵% می‌باشند. احتمال اینکه یک پیغام انتخاب شده به صورت تصادفی، تبلیغ(هرزنامه) باشد چقدر است؟

به منظور پاسخ به این سوال، با توجه به نمادهای تعریف‌شده در ذیل و درصدهای داده شده داریم:

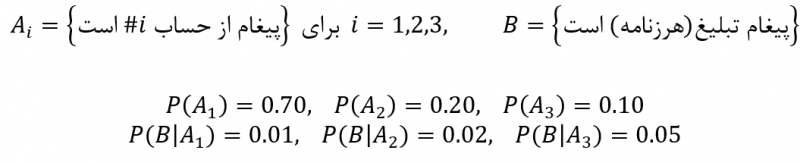
حال به سادگی داریم:

P(B)=(0.01)(0.7) + (0.02)(0.2) + (0.05)(0.1) = 0.016

یعنی در بلند مدت، ۱.۶% از پیغام‌های این شخص تبلیغ(هرزنامه) خواهند بود.

قانون بیز

فرض کنید که A_۱, A_۲, …, A_k یک مجموعه kتایی از پیشامدهای ناسازگار و جامع با احتمالات پیشین (i=1,2,…k ) P(A_i ) باشند. سپس برای هر پیشامد دیگر B که برای آن P(B)>0، احتمال پسین A_j در صورت رخ دادن B برابر است با:

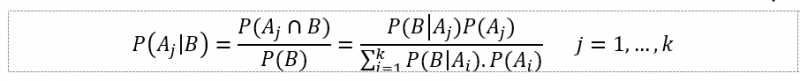
محاسبه فوق بر مبنای استفاده از قانون ضرب در صورت و قانون احتمال کامل در مخرج است. زیاد شدن پیشامدها، می‌تواند برای تازه‌واردان علم احتمال اندکی دشوار باشد. تا زمانی که پیشامدهای اندکی در کسر وجود دارد، یک نمودار درختی می‌تواند به عنوان مبنای محاسبات احتمالات پسین بدون حتی اشاره مستقیم به قاعده بیز به کار گرفته شود.

مثال۲:

از هر ۱۰۰۰ بزرگسال تنها ۱ نفر مبتلا به یک بیماری نادر است که آزمایش تشخیصی برای آن کشف شده است. این آزمایش به گونه‌ای است که وقتی فرد در واقع به این بیماری مبتلا باشد، نتیجه ۹۹% مواقع مثبت خواهد بود، در حالی که برای یک فرد بدون بیماری تنها ۲% از مواقع آزمایش نتیجه مثبت را نشان خواهد داد. (به عبارتی شاخص “حساسیت(Sensitivity)” آزمایش ۹۹% و شاخص “اختصاصی‌بودن(Specificity)” آن ۹۸% است؛ در مقابل، Sept22, 2012 issue of The Lancet گزارش می‌کند که اولین آزمایش خانگی HIV، “حساسیت” ۹۲% و “اختصاصی‌بودن” ۹۹.۹۸% را دارد). اگر روی یک شخص که به صورت تصادفی انتخاب شده، آزمایش صورت گیرد و نتیجه مثبت باشد، احتمال اینکه این فرد بیمار باشد چقدر است؟ 

برای استفاده از قاعده بیز، فرض کنید  “فرد بیمار است=A_۱“، “فرد بیمار نیست=A_۲” و “نتیجه آزمایش مثبت است=B”. پس خواهیم داشت: P(A_۲)=۰.۹۹۹, P(A_۱)=۰.۰۰۱, P(B|A_۱)=۰.۹۹, P(B|A_۲)=۰.۰۲ و نمودار درختی برای این مساله در شکل زیر آورده شده است.

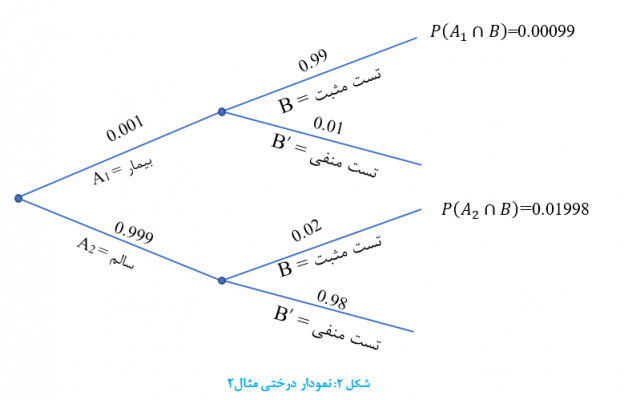
بنابراین، ۰.۰۲۰۹۷ = ۰.۱۹۹۸ + ۰.۰۰۰۹۹=(P(B که از آن داریم:

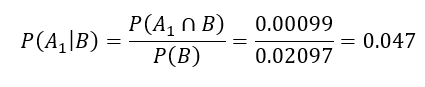
این نتیجه خلاف واقعیت به نظر می‌رسد؛ آزمایش تشخیصی چنان دقیق به نظر می‌رسد که انتظار داریم کسی که نتیجه آزمایش مثبت داشته، به احتمال زیاد مبتلا به این بیماری باشد؛ در حالی که احتمال مشروط محاسبه شده تنها ۰.۰۴۷ است. با این حال، نادربودن بیماری دلالت بر این دارد که بیشترین نتایج آزمایش مثبت ناشی از خطاهاست تا افراد بیمار. در این مثال احتمال داشتن بیماری ۴۷ برابر شده است. (از پیشین ۰.۰۰۱ به پسین ۰.۰۴۷)؛ اما برای رسیدن به افزایش بیشتر در احتمال پسین، یک آزمایش تشخیصی با نرخ خطای بسیار کمتر نسبت به این نوع آزمایش مورد نیاز است.