مقالات آمار و احتمال
منحنیهای OC

در تعیین اندازه نمونه، استفاده از منحنیهای OC راحتتر از روش تحلیلی است. این منحنیها مقدار β را بر حسب پارامتر d برای اندازههای مختلف نمونه یا همان n نشان میدهند. منحنیهای OC با توجه به یک طرفه یا دو طرفه بودن آزمون و در سطح معناداری مشخص α ترسیم میشوند. پارامتر d برای آزمون حالت ۱-۱ به صورت زیر تعریف شده است:
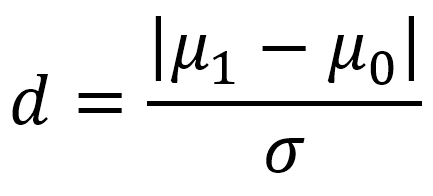
- هر چه مقدار واقعی میانگین یا همان μ۱ از مقدار مشخص شده در فرض صفر یا همان μ۰ دورتر باشد، احتمال خطای نوع دوم یا β به ازای n و α ثابت کمتر میشود، یعنی کشف تفاوتهای بزرگ در میانگین آسان تر از کشف تفاوتهای کوچک است.
- برای مقادیر d و α ثابت، احتمال خطای نوع دوم یا β با افزایش n کاهش مییابد. به این معنی که اگر میانگین واقعی برابر μ۱ باشد، برای کشف تفاوت میان مقدار ادعایی فرض صفر با میانگین واقعی، با افزایش اندازه نمونه، آزمون را قویتر میکنیم.
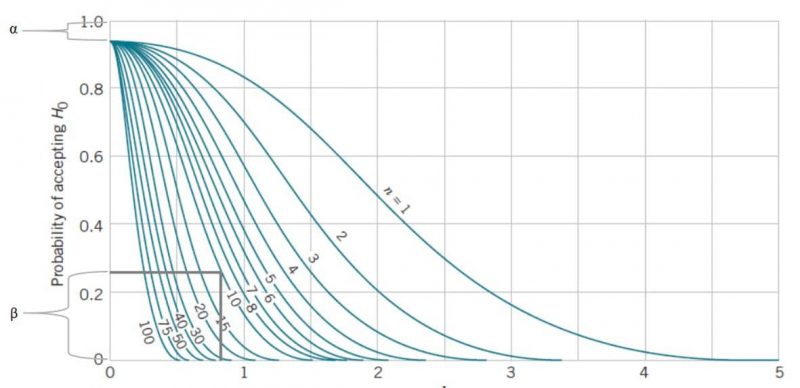
به طور کلی، منحنیهای مشخصه عملیاتی (OC) شامل سه پارامتر β، d و n هستند. با داشتن هر دو مورد از این پارامترها، میتوان مقدار سومی را تعیین کرد. محور افقی منحنی بر حسب مقدار پارامتر d و محور عمودی بر حسب احتمال عدم رد فرض صفر میباشد. با توجه به نمودار، احتمال عدم رد فرض صفر در نقطه شروع منحنیها، حداکثر میتواند برابر (α)-۱ باشد.
برای درک بهتر:
- در صورتی که میانگین واقعی به طور حدی به سمت مقدار مشخص شده در فرض صفر متمایل شود، مقدار β برابر (α)-۱ خواهد بود و احتمال عدم رد فرض صفر در بیشترین حالت است. البته در واقع چنین تعریفی نادرست است و روی نمیدهد زیرا با توجه به پیشفرض قبلی که از β داشتیم احتمال رد نکردن فرض صفر با وجود نادرست بودن آن در نظر گرفته میشود که در صورت قرار گرفتن میانگین واقعی در بازه عدم رد فرض صفر دیگر خطایی رخ نداده است. حال از سمت دیگر، با دورتر شدن میانگین واقعی از مقدار مشخص شده در فرض صفر، میزان β کاهش پیدا کرده و احتمال عدم رد فرض صفر نیز به همان میزان کاهش مییابد.
- در صورتی که میانگین واقعی از مرز رد و عدم رد فرض صفر عبور کند، این میزان β که حکم خطا را دارد برای ما حیاتی میشود چرا که عدم رد فرض صفر یک تصمیم نادرست است و هر عضو قرار گرفته از توزیع میانگین واقعی درون حدود عدم رد فرض صفر به احتمال عدم رد فرض صفر با وجود نادرست بودن آن میافزاید و ما خواهان کشف چنین خطایی هستیم. طبیعتا مشاهدهی اعضای توزیع میانگین واقعی درون بازه عدم رد فرض صفر ناشی از پراکندگی توزیع است.
- در صورتی که میانگین واقعی به شدت از مقدار مشخص شده در فرض صفر دور شود، مقدار β و به تبع آن میزان احتمال عدم رد فرض صفر به شدت کاهش خواهد یافت و به صفر میل میکند. بنابراین احتمال رد فرض صفر بسیار بالا رفته و کشف چنین اختلافی بسیار محتمل و قابل پیش بینی است. هرچند بدلیل پراکندگی دادهها بطور قطعی نمیتوان گفت که دقیقا صفر است.
با توجه به این توضیحات بالا میتوان نتیجه گیری کرد که دلیل عنوان کردن محور عمودی بر حسب احتمال عدم رد فرض صفر این است که بسته به فاصلهی موجود میان میانگین واقعی و مقدار مشخص شده در فرض صفر، اگر این میزان خارج بازه عدم رد فرض صفر قرار داشته باشد β خواهد بود و در غیر این صورت خطای نوع دوم رخ نداده و مقدار روی محور فقط برابر همان احتمال عدم رد فرض صفر است.
دو کاربرد متداول برای این منحنیها وجود دارد:
- یافتن β به ازای مقادیر ثابت d و n داده شده. در چنین شرایطی تحلیلگران نگران ریسک آزمونی هستند که قبلاً صورت گرفته و اکنون درباره میزان توان آزمون مطالعه انجام میدهند. این شرایط معمولا زمانی رخ میدهد که اندازه نمونه توسط عوامل اقتصادی یا سایر عوامل محدود شده است.
- یافتن n به ازای مقادیر ثابت β و d داده شده. تحلیلگران معمولاً زمانی با این مساله مواجه می شوند که فرصت انتخاب اندازه نمونه را در ابتدای آزمایش داشته باشند.
نکته: استفاده از منحنیهای OC نتایج دقیقتری خواهد داشت، زیرا در روش تحلیلی ما دست به یک تقریب زدیم اما در این روش پارامترها با روشهای محاسبات عددی بدست آمدهاند.
برای دانلود فایل منحنیهای OC روی لینک زیر کلیک کنید.
