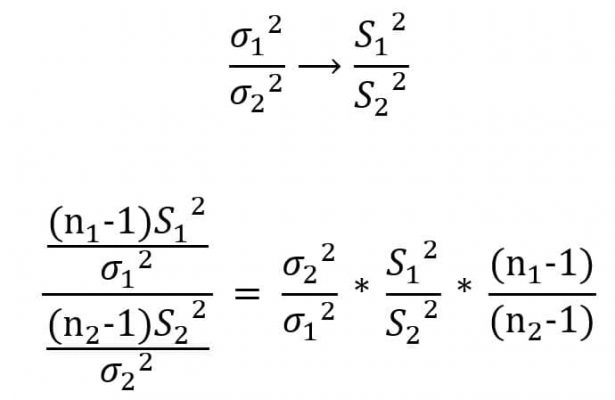مقالات آمار و احتمال
مقایسه دو نمونه آماری و مقایسه واریانس دو جامعه
یکی از موارد مهم و کاربردی در آمار بررسی و مطالعه تفاوتها در عملکرد است. فرض کنید X و Y دو متغیر تصادفی باشند و x۱, x۲, …, xnx نمونههایی از X
و y۱, y۲, …, yny نمونههایی از Y باشند. آنگاه:

برای مقایسه این دو متغیر تصادفی از عمل تفریق استفاده مینماییم.

حال از متغیرهای تصادفی X و Y، توزیع مربع کای میسازیم سپس این دو متغیر تصادفی را با هم جمع کرده تا یک توزیع مربع کای در نهایت داشته باشیم.
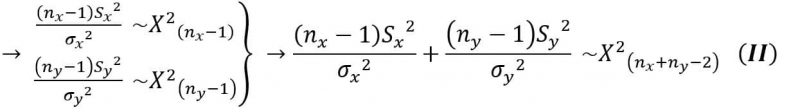
حال یک توزیع نرمال استاندارد و یک مربع کای داریم و با استفاده از این دو میتوانیم متغیری تصادفی دارای توزیع t بسازیم.
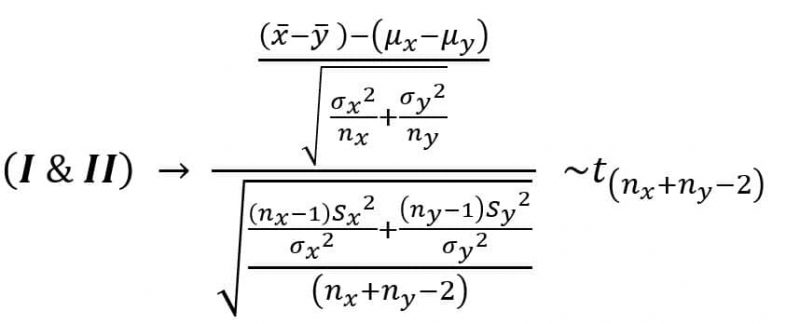
Table of Contents
حالت خاص
شرایطی که واریانسهای دو نمونه با یکدیگر برابر باشند. σ۲=σ۲y=σ۲x
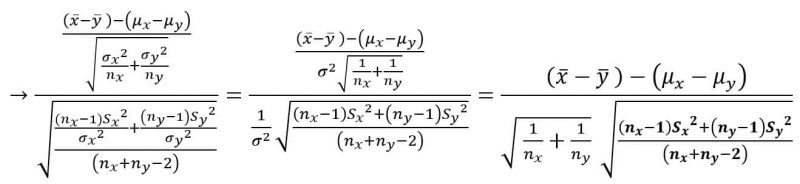
واریانس نمونهای مشترک
در حالتی خاص از بررسی تفاوت دو نمونه، در صورتی که تنها بدانیم واریانسهای دو جامعه با یکدیگر برابر هستند، برای تخمین واریانس جامعه (که مجهول است) از برآوردگری با نام واریانس نمونهای مشترک استفاده میکنیم. در این برآورد با استفاده از ضرایب وزنی که مرتبط با اندازهی هر نمونه هستند، از اطلاعات هر دو نمونه استفاده میشود تا برآوردگری نااریب و مناسب بدست بیاید. طبیعتا نمونهای که حجم بیشتری دارد تاثیری بیشتری در واریانس میگذارد. 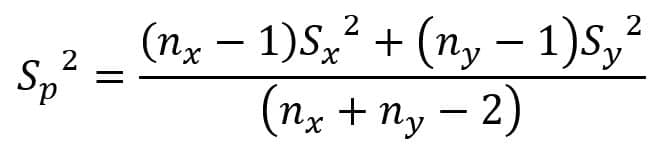
که این مقدار دقیقا برابر عبارت زیر رادیکال در حالت خاصی است که درباره آن صحبت کردیم. شکل سادهتر شده آن به صورت زیر میباشد.
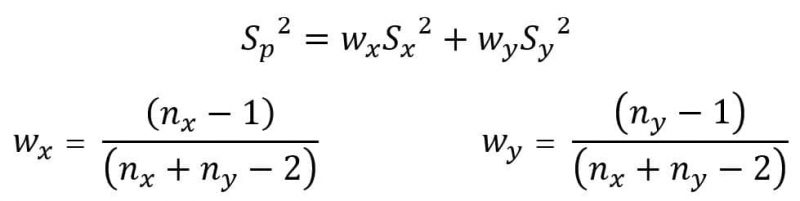
سوال: آیا S۲p نااریب است؟ و چرا به جای آن از عبارت زیر استفاده نکنیم؟
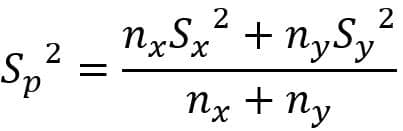
مقایسه واریانس
میتوان برای تخمین نسبت واریانسهای دو جامعه از نسبت واریانسهای نمونهی آنها استفاده کرد. با توجه به این قضیه نسبت دو متغیر تصادفی مربع کای اهمیت پیدا میکند و زمینهای برای یک توزیع جدید میشود.