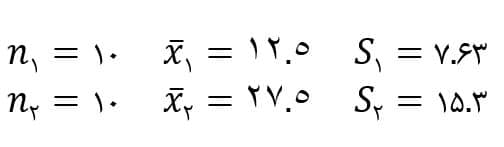مقالات آمار و احتمال
حالت ۲-۲) آزمون فرض و فاصله اطمینان برای مقایسهی میانگین دو توزیع نرمال در صورت مجهول بودن واریانسها
ویدوی آموزشی برای حالت ۲-۲-۱
ویدوی آموزشی برای حالت ۲-۲-۲
حالت خاص ۲-۲-۱) برابر بودن واریانسها:
σ۱۲=σ۲۲=σ
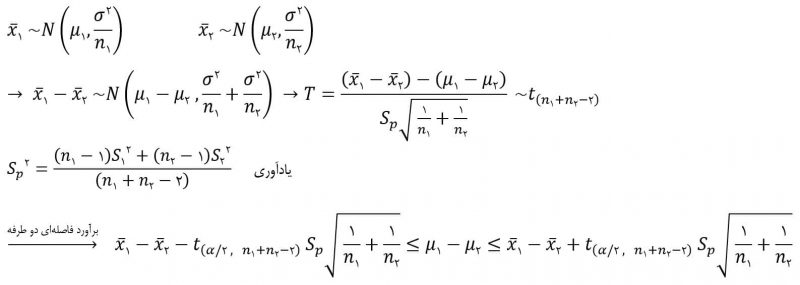
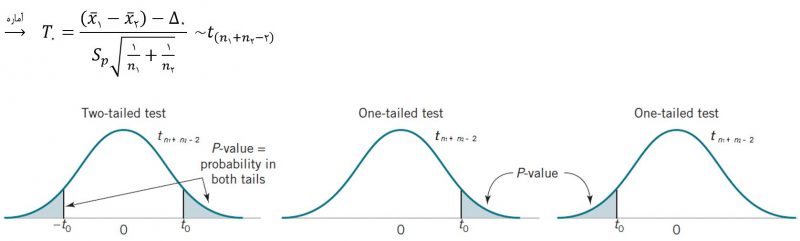
مثال: دو کاتالیست مورد آزمایش قرار گرفته اند و بر اساس آزمایش انجام شده نتایج زیر بدست آمده است:

در شرایط فعلی از کاتالیست شماره ۱ استفاده میشود اما کاتالیست شماره ۲ نیز قابل قبول است. کاتالیست شماره ۲ ارزان تر است اما در صورتی مجاز به استفاده از آن هستیم که در بازده فرآیند شیمیایی تاثیر قابل توجهی نداشته باشد. اگر واریانس دو کاتالیست برابر باشد، تفاوتی در میانگین بازده مشاهد میکنید؟ سطح معناداری را ۵ درصد در نظر بگیرید.

حالت خاص ۲-۲-۲) نابرابری واریانسها:
در صورتی که درجه آزادی توزیع بصورت عدد صحیح بدست نیامد، مقدار حاصل را گرد میکنیم.
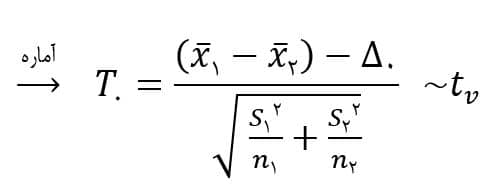
مثال. غلظت آرسنیک در منابع آب آشامیدنی عمومی یک خطر بالقوه برای سلامتی است. در رابطه با دو منطقه تست سنجش میزان آرسنیک در آب آشامیدنی انجام شده است. میخواهیم تفاوت بین میزان آرسنیک در آب دو منطقه را مورد بررسی قرار دهیم. نتایج نمونه گیری به شرح زیر است
در سطح معناداری ۵ درصد آزمون را اجرا کنید.

نکته: با توجه به نتیجه آزمون فرض دو طرفه روی برابری و اطلاعات بدست آمده از نمونهگیری، میتوان روی کمتر بودن یا بیشتر بودن نیز نظر داد. برای مثال در این آزمون نتیجه بر نابرابر بودن دو میانگین حکم کرد. از طرف دیگر، طبق شواهد مساله، میانگین نمونه منطقه دوم بیشتر است که این یعنی میانگین غلظت آرسنیک در آب آشامیدنی منطقه دوم بیشتر است.