مقالات آمار و احتمال
برآورد فاصلهای میانگین توزیع نرمال در صورت معلوم بودن واریانس
مفهوم اساسی یک فاصله اطمینان با در نظر گرفتن یک موقعیت ساده به راحتی قابل درک است. فرض کنید که ما یک جامعه نرمال با میانگین ناشناخته و واریانس شناخته شده داریم. این شرایط تا حدی غیر واقعیست زیرا معمولاً هر دو پارامتر ناشناخته هستند.
میدانیم که میانگین نمونه از توزیع نرمال با میانگین μ و واریانس σ۲/n پیروی میکند، بنابراین میتوانیم متغیر تصادفی Z را با توزیع نرمال استاندارد بصورت زیر بدست آوریم.
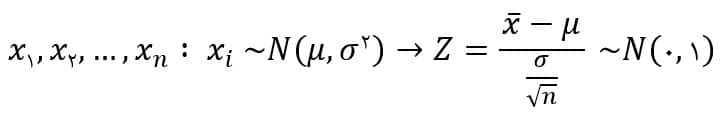
فاصله اطمینان تخمینی برای میانگین بصورت بازهای با حد بالا و حد پایین خواهد بود که این نقاط انتهایی بازه با استفاده از اطلاعات نمونه محاسبه میشوند.
![]()
با توجه به اینکه نمونه گیریهای مختلف، نقاط پایان بازهی مختلفی ایجاد میکنند، این نقاط پایانی متغیرهای تصادفی L و U هستند. فرض کنید که می توانیم مقادیر L و U را به گونه ای تعیین کنیم که احتمال زیر درست باشد:
![]()
مقدار ۱-a ضریب اطمینان بازه نام دارد و از جنس احتمال است. ضریب اطمینان نشان میدهد که با این احتمال، میانگین واقعی در این بازه قرار دارد و معمولا ۹۵% در نظر گرفته میشود.
در چنین شرایطی، از آنجا که Z از توزیع نرمال پیروی میکرد میتوانیم بنویسیم:
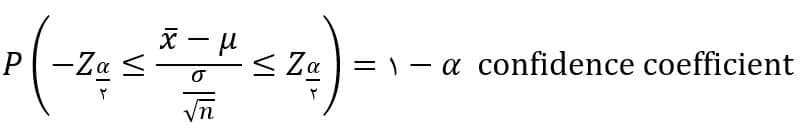
در ادامه با تنها کردن μ به بازه زیر میرسیم:
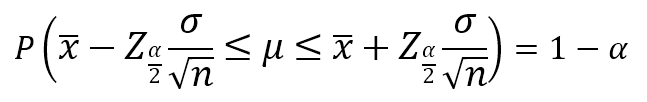
با این تفاسیر، یک بازه تصادفی با توجه به نقاط پایانی بازه که متغیرهایی تصادفی هستند بدست میآید که بصورت زیر تعریف میشود:
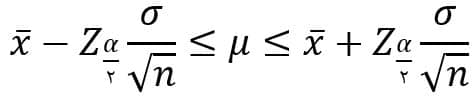
شمایل کلی یک بازه برآورد فاصلهای به صورت زیر است:

بنابراین برآوردگر فاصلهای حصاری به دور برآوردگر نقطهای است.
مثال: با توجه به نمونههای بدست آمده از وزن کیسههای برنج یک انبار، یک برآورد فاصلهای با ضریب اطمینان مناسب برای میانگین وزن کل کیسههای برنج انبار بدست آورید. انحراف معیار کل برابر یک میباشد.
۶۴.۱ ۶۴.۶ ۶۴.۷ ۶۴.۸ ۶۴.۵ ۶۴.۲ ۶۴.۳ ۶۴.۲ ۶۴.۳ ۶۴.۳
پاسخ: ابتدا میانگین نمونه (برآوردگر نقطهای) را محاسبه میکنیم. ضریب اطمینان را ۹۵ درصد در نظر میگیریم.
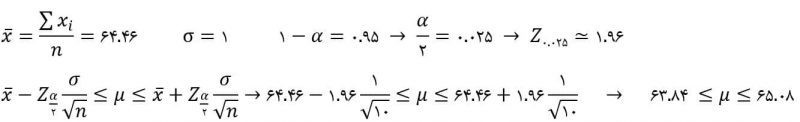
کنترل میزان خطا و اندازه مطلوب نمونه:
اگر توجه کرده باشید، در بدست آوردن بازه اطمینان، ضریب اطمینان بصورت دلخواه ۹۵ درصد انتخاب شد. شاید به این مورد فکر کنید که چرا اطمینان را بیشتر نکنیم؟ برای مثال بازه اطمینانی با ضریب ۹۹ درصد را در نظر بگیرید و آن را با بازه اطمینان ۹۵ درصدی مقایسه کنید. از آنجا که مقدار Z(α/۲) به ضریب اطمینان بستگی دارد، طول دو بازه با یکدیگر متفاوت خواهد بود.
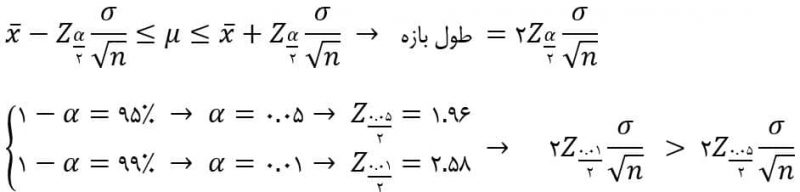
بنابراین طول بازه اطمینان ۹۹ درصدی، بیشتر از طول بازه ۹۵ درصدی خواهد بود. در واقع هرچه اطمینان بیشتر باشد، طول بازه نیز بیشتر خواهد بود.طول یک بازه اطمینان بیانگر میزان دقت آن بازه در برآورد پارامتر مجهول است. برای مثال، یک بازه برای ساعت صرف ناهار را در نظر بگیرید. بازه ساعات ۵:۰۰ تا ۲۲:۰۰ از اطمینان شدیدا بالایی برخوردار است اما نتیجه مطلوبی نخواهد داشت. در نقطه مقابل، بازه ساعات ۱۳:۰۰ تا ۱۴:۳۰ را در نظر بگیرید. با اینکه از اطمینان کمتری برخوردار است اما نتیجه، اطلاعاتی مفید را به ما ارائه میدهد.
از نتیجهگیری قبل دانستیم که طول بازه با ضریب اطمینان رابطهای معکوس دارد که نشان میدهد فاصله اطمینانی که به دست آید باید به اندازه کافی برای اهداف تصمیمگیری کوتاه باشد و همچنین از اطمینان کافی برخوردار باشد.

طول بازه اطمینان برابر حداکثر فاصله پارامتر مجهول تا برآوردگر نقطهای میباشد و از آنجا که مقدار واقعی خطا (اختلاف برآوردگر نقطهای و پارامتر مجهول) مجهول است، طول بازه اطمینان به عنوان حداکثر خطا کاربرد دارد. حداکثر خطا به ضریب اطمینان، اندازه نمونه و واریانس بستگی دارد. واریانس بیشتر نشان دهنده پراکندگی دادهها و نوسانات بیشتر پدیده خواهد بود که طبیعتا خطای برآورد را افزایش خواهد داد. از آنجا که عموما ضریب اطمینان برای آزمایش کننده معین شده است، فقط اندازه نمونه دارای حق انتخاب میباشد بنابراین تخمین اندازه مطلوب نمونه از اهمیت بالایی برخوردار میگردد.
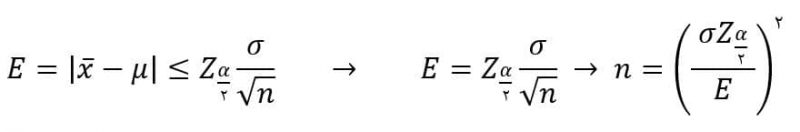
مثال: در رابطه با مثال قبلی، در صورتی که حداکثر خطای قابل انتظار ۰.۵ کیلو باشد، اندازه مناسب نمونه را بدست آورید.
پاسخ:
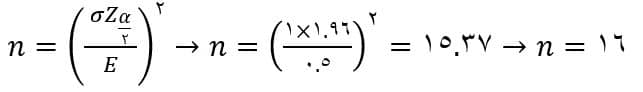
نکته: اگر اندازه نمونه به سمت پایین گرد شود خطا از حداکثر تعیین شده بیشتر میشود. در واقع عدد بدست آمده حداقل اندازه نمونه برای رعایت حداکثر خطاست. پس به سمت بالا عدد را گرد کنید.
