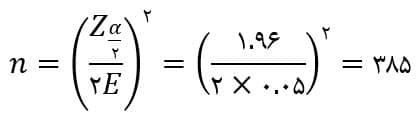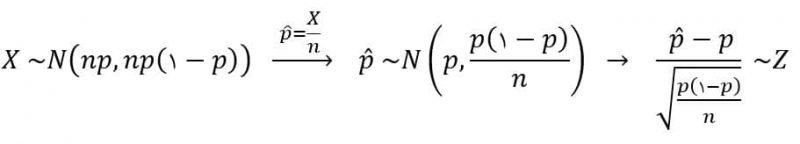مقالات آمار و احتمال
برآورد فاصلهای برای نسبت جامعه
فرض کنید که یک نمونه تصادفی با اندازه n از یک جامعه بزرگ گرفته شده است و مشاهدات X در این نمونه متعلق به یک زیر مجموعه دلخواه از این جامعه است. پس p=x/n یک برآوردگر نقطهای برای p یا همان نسبت واقعی از جامعه است که به این زیر مجوعه تعلق دارد. باید توجه داشت که n و p پارامترهای یک توزیع دو جملهای هستند و X از توزیع دو جملهای پیروی میکند.
X~Bin(n,p)
تقریب نرمال از توزیع دو جملهای:
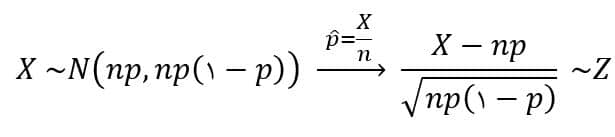
با شرایط زیر، توزیع X با میانگین np و واریانس np(1-p) تقریباً نرمال است:
- اگر p خیلی نزدیک به ۰ یا ۱ نباشد. چرا؟ تا مخرج نرمال استاندارد صفر نشود.
- اگر n نسبتاً بزرگ باشد. چرا؟ تقریب با دقت خوبی انجام شود.

متغیر تصادفی اولیه برای یک برآورد فاصلهای به دست آمده اما مجهول بودن پارامتر P کار را با کمی مشکل دچار میکند.
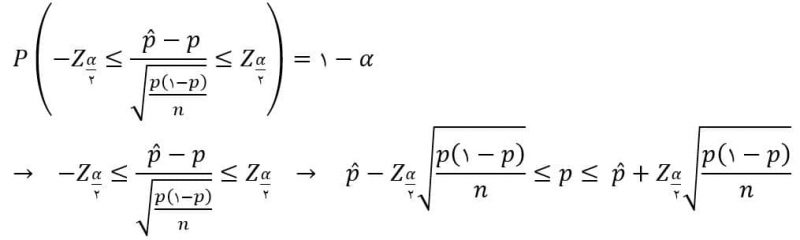
حال برای رفع مشکل مجهول بودن پارامتر P از تقریب زیر استفاده میکنیم.
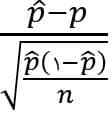

مثال: یک فرآیند نمونهگیری از ۸۵ خودرو را در نظر بگیرید. ۱۰ مورد از این نمونهها، پارامترهای مورد انتظار را از نظر فنی برآورد نکردهاند. یک فاصله اطمینان %۹۵ دو طرفه برای نسبت موتورهای معیوب بدست آورید.
پاسخ:
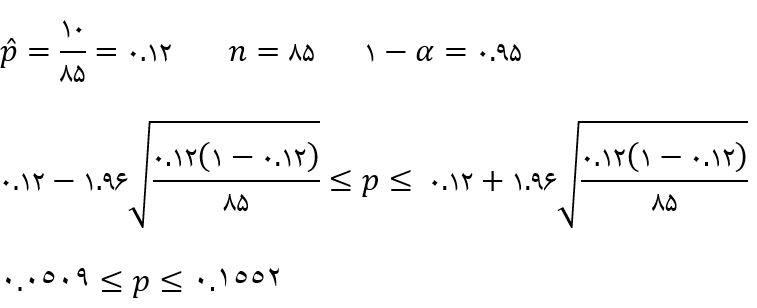
کنترل میزان خطا و تعیین اندازه نمونه:
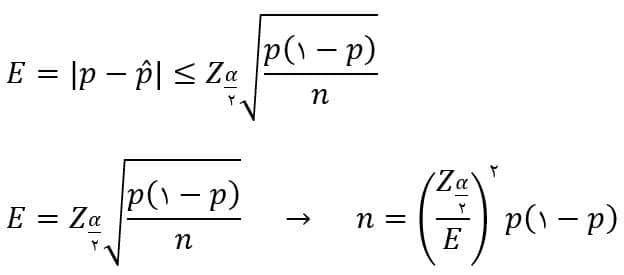
از آنجا که پارامتر P مجهول است، میتوان با تقریب Phat خطای تقریبی را بدست آورد. اما در صورتی که هنوز برآوردی از P نداشته باشیم میتوان حداکثر خطای ممکن را در نظر گرفت: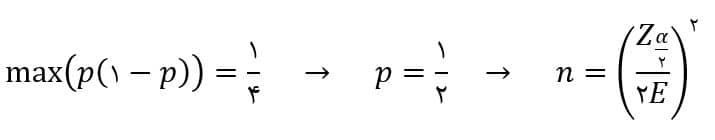
مثال: با توجه به مثال قبلی،
الف) اگر در نظر باشد میزان خطا کمتر از ۰.۰۵ شود، با توجه به نمونههای قبلی، چه تعداد نمونه دیگر نیاز است؟
ب) با فرض اینکه هیچ نمونه گیری سابقی نداشته باشیم، با میزان خطای کمتر از ۰.۰۵، اندازه نمونه را بدست آورید.
پاسخ: الف)
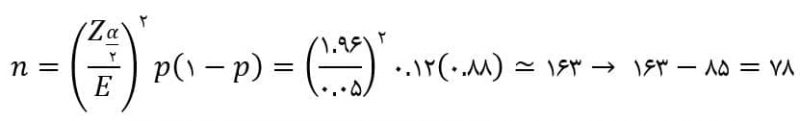
ب)