آزمون فرض یک پارامتری (Hypothesis Testing)

در برآورد فاصله‌ای نشان داده شد که چگونه یک پارامتر از جامعه را می‌توان با داده‌های نمونه، بصورت یک بازه‌ تخمین زد. در موقعیتی متقابل، نوع دیگری از مساله در زمینه استنتاج آماری روی می‌دهد. ادعاهایی در مورد پارامتری از جامعه وجود دارد و باید با استفاده از داده‌های نمونه، ادعای درست را تعیین کرد.

فرض آماری:

یک فرضیه‌ آماری گزاره‌ای درباره پارامترهای یک یا چند جامعه آماری می‌باشد. در یک مثال ساده می‌توان میانگین حجم آب بطری‌های تولیدی یک شرکت آب معدنی را به عنوان پارامتر مورد مطالعه در نظر گرفت. برابری میانگین حجم آب بطری‌ها با یک مقدار مشخص، یک فرضیه آماری است.

مثال بالا را در نظر بگیرید. در برآورد فاصله‌ای با استفاده از شواهد و اطلاعات نمونه به یک بازه برای میانگین حجم آب بطری‌ها دست می‌یافتیم. حال در آزمون فرض آماری با روی دیگر سکه روبرو هستیم. شرکت مورد نظر ادعا دارد که میانگین حجم آب بطری‌ها μ_۰ است. این عبارت یک فرض آماری خواهد بود. اما بررسی و آزمایش صحت آن یک آزمون فرض آماری است. بنابراین در آزمون فرض آماری، درستی یا نادرستی یک ادعا قضاوت می‌شود. از آنجا که در آمار، توزیع جوامع واقعی با توزیع‌های احتمالی ارائه می‌شود، معیار و مبنای آزمون فرض نیز توزیع احتمالی نمونه‌های تصادفی است.

فرض صفر یا H_۰ ادعایی است که در ابتدا درست در نظر گرفته می‌شود. فرض‌های صفر همیشه عبارتی درباره برابری پارامتر جامعه با مقداری خاص می‌باشند. برای بیان رسمی فرض در مثال حجم آب بطری داریم:

فرض صفر یا H_۰ ادعایی است که در ابتدا درست فرض می‌شود. در مثال حجم آب بطری داریم:

عبارت پایین نیز فرض یک یا فرضیه جایگزین نام دارد و گزاره‌ای است که مقابل و در تناقض با فرض صفر است. فرض صفر و فرض یک هیچگونه اشتراکی ندارند و هیچگاه هر دو گزاره نمی‌توانند درست باشند.

این فرض آماری به عبارتی بیان می‌کند که مقدار μ بالاتر یا پایین‌تر از μ_۰ است. بنابراین می‌توان گفت که یک فرض جانشین دو طرفه است. در حالت کلی، فرض یک می‌تواند دو طرفه یا یک طرفه باشد.

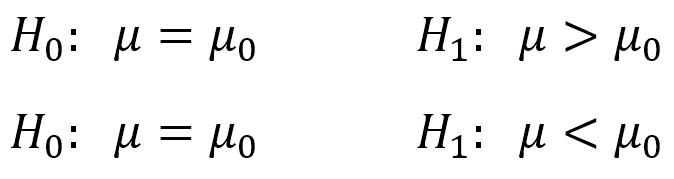
همانطور که گفته شد، فرض صفر همواره در هر دو حالت یک طرفه و دو طرفه، یک گزاره برابری می‌باشد، اما با این حال می‌توان فرض صفر را بطور ضمنی بصورت زیر در نظر گرفت که مشکلی ایجاد نمی‌کند:

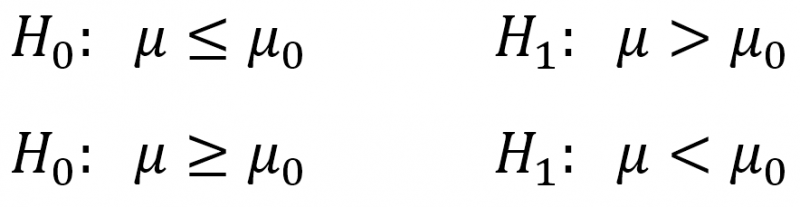
نکته مهم دیگر در مورد فرض‌های آماری این است که هیچگاه یک فرض آماری درباره نمونه یا آماره‌ای از نمونه نمی‌باشد و همواره گزاره‌ای شامل پارامتر جامعه و مقدار معین ادعایی می‌باشد.

این مقادیر مشخص شده ادعایی که با اندیس صفر نمایش داده می‌شوند، معمولا از روش‌های زیر تعیین می‌شوند:

• تجربه گذشته، شناخت از فرآیند و یا حتی آزمایش‌ها و آزمون‌های فرض قبلی
• نظریات تئوری، مدل‌ها و استانداردها یا تعهدات قراردادی

آزمون فرض آماری:

روشی که منجر به تصمیم گیری و قضاوت درباره فرض صفر می‌شود آزمون فرض نام دارد. آزمون فرض بر اساس اطلاعات نمونه تصادفی از جامعه هدف مطالعه انجام می‌گردد. در صورتی که این اطلاعات بر فرض صفر استوار باشد، فرض صفر رد نخواهد شد اما اگر اطلاعات با فرض صفر در تناقض باشد، نتیجه خواهیم گرفت که فرض صفر رد می‌شود و فرض جانشین صحیح است. درستی و نادرستی فرض صفر هیچگاه بطور قطعی بیان نمی‌شود مگر اینکه جامعه بطور کامل بررسی گردد. اما چنین موقعیتی اغلب نشدنی می‌باشد و بنابراین، آزمون فرض به همراه احتمال رسیدن به یک نتیجه نادرست یا همان خطا ارائه می‌گردد. آزمون فرض شامل گرفتن نمونه تصادفی، محاسبه آماره با استفاده از اطلاعات نمونه و سپس استفاده از آماره آزمون برای تصمیم گیری در مورد فرضیه صفر است.

در مثال دیگری فرض کنید ادعا شده است که میانگین طول قطعات تولیدی یک کارخانه ۵۰cm است. میانگین نمونه یا Xbar تخمینی از میانگین واقعی است و در صورتی که نزدیک به مقدار  M=50cm باشد تضادی با فرض صفر ندارد اما اگر میانگین نمونه تفاوت قابل توجهی با مقدار ۵۰cm داشته باشد شواهدی در حمایت از فرض یک وجود دارد که منجر به رد ادعا می‌گردد. در این مثال، میانگین نمونه آماره‌ی آزمون است.

فرض کنید اگر Xbar در بازه بین ۵۱.۵ و ۴۸.۵ فرض صفر رد نمی‌شود یا به عبارتی این فاصله برای میانگین نمونه، ناحیه رد نشدن فرض صفر باشد. مقادیر ۴۸.۵ و ۵۱.۵ مقادیر بحرانی نامیده می‌شوند. در این صورت بازه‌های ۴۸.۵>Xbar و ۵۱.۵<Xbar  برای میانگین نمونه، منجر به رد فرض صفر می‌گردد و این فواصل، ناحیه رد شدن فرض صفر نامیده می‌شوند.نمونه‌های تصادفی می‌توانند مقادیر مختلفی باشند. اگر میانگین واقعی طول قطعات همان ۵۰cm باشد اما نمونه‌های تصادفی گرفته شده در ناحیه رد فرض صفر قرار بگیرند، فرض صفر رد می‌شود در حالی که واقعا صحیح است. به این تصمیم گیری نادرست، خطای نوع اول گفته می‌شود.

حال فرض کنید که میانگین واقعی طول قطعات با ۵۰Cm متفاوت است، با این حال میانگین نمونه در ناحیه پذیرش قرار بگیرد. در این صورت با وجود نادرستی H_۰ ، در رد کردن آن شکست می‌خوریم و این منجر به خطای نوع دوم می‌شود.

بنابراین تصمیم گیری در آزمون فرض می‌تواند شامل موقعیت‌های زیر باشد:

خطای نوع اول:

در مثال قطعات، انحراف استاندارد طول قطعات را در شرایطی که از توزیع نرمال پیروی می‌کنند σ=۲.۵ و اندازه نمونه را n=10در نظر بگیرید.

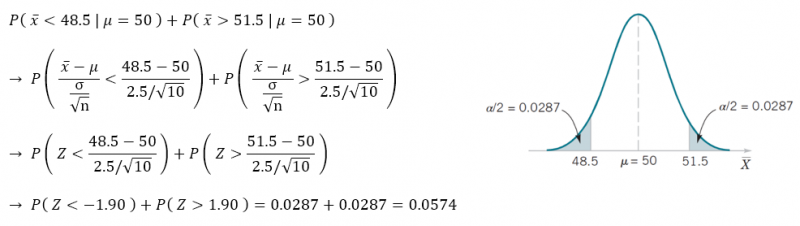
این احتمال، خطای نوع اول یا سطح معناداری نام دارد که برابر α است و در هر آزمون یک حالت دارد. در صورتی که بازه پذیرش تغییر کند، خطای نوع اول نیز تغییر خواهد کرد. با توجه به شکل بالا واضح است که با بزرگ تر کردن بازه پذیرش، مساحت α کمتر می‌شود و خطای نوع اول کاهش می‌یابد. در مفهوم، خطای نوع اول یعنی اینکه ما چه میزان تمایل به پذیرفتن شواهد بر علیه فرض صفر داریم و سطح اهمیت و معناداری داده‌ها برای رد فرض صفر چقدر هستند. برای مثال برخورد یک گربه به خودرو چندان به فرض سالم بودن خودرو شکی وارد نمی‌کند اما برخورد یک خودروی دیگر با آن فرض عدم آسیب دیدن خودرو را زیر سوال میبرد و مهم است. در مثال قطعات نیز اختلاف های بیشتر از ۱.۵cm با ادعا، معنادار در نظر گرفته شده اند و موجب رد فرض صفر می‌شوند اما تفاوت‌های کمتر از ۱.۵cm برای رد فرض صفر کافی نبوده‌اند.

نمونه زیر را در نظر بگیرید.

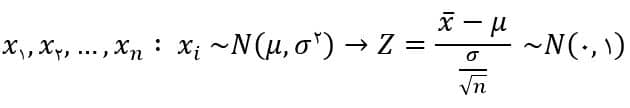
در صورتی که Μ=M_۰ در نظر گرفته شود، با دانسته‌های برآورد فاصله‌ای، بازه‌ای برای میانگین نمونه تخمین می‌زنیم.

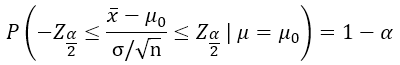
به این ترتیب بازه عدم رد فرض صفر به صورت زیر:

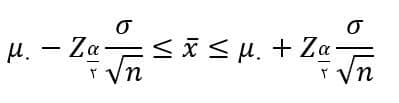
و بازه رد فرض صفر نیز به شکل زیر خواهد بود:

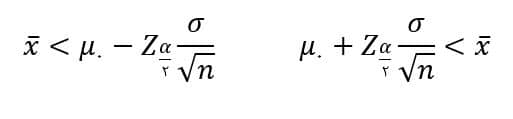
بدست آوردن احتمال خطای نوع اول:

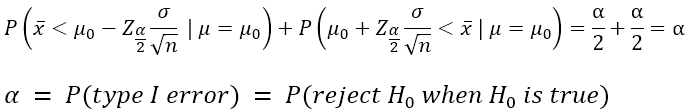
بازه پذیرش استاندارد و آماره آزمون:

از آنجا که با تغییر اطلاعات نمونه و فرض صفر، بازه پذیرش مذکور نیز تغییر خواهد کرد، برای راحت تر شدن کار بازه پذیرش را بر اساس مقادیر توزیع احتمالی معادل می‌کنیم که در این صورت با تغییر اطلاعات نمونه و فرض صفر، بازه تغییر نخواهد کرد و تنها آماره آزمون تغییر خواهد داشت.

آماره تابعی از نمونه‌های تصادفی است و مقدار آن قابل محاسبه هستند. آماره آزمون بر اساس اطلاعات نمونه و مقدار مشخص شده در فرض صفر بدست می‌آید که همگی معلوم هستند.

در این آزمون فرض، متغیر تصادفی Z_۰ زیر با مقدار مشخص شده در فرض صفر μ_۰ معلوم می‌شود و آماره آزمون خواهد بود.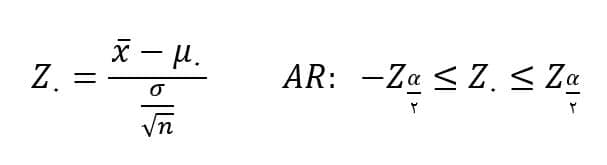

خطای نوع دوم:

در ارزیابی یک آزمون فرض، بررسی احتمال خطای نوع دوم نیز مهم است که آن را با β نشان می‌دهیم. این نوع خطا، بر خلاف خطای نوع اول که به ازای تمام مقادیر واقعی پارامتر مجهول یکسان بود، وابسته به پارامتر مجهول است و برای محاسبه آن همیشه باید یک فرض یک ویژه داشته باشیم.

در مثال قطعات تولیدی کارخانه، فرض کنید میانگین واقعی طول قطعات ۵۲cm و بازه پذیرش Xbar بین ۵۱.۵ و ۴۸.۵ باشد. . بنابراین این امکان وجود دارد که میانگین نمونه در بازه پذیرش قرار بگیرد و فرض صفر با وجود نادرست بودن رد نشود و خطای نوع دوم رخ بدهد. توجه کنید که هر چه میانگین واقعی از مقدار مشخص شده در فرض صفر دورتر باشد احتمال خطای نوع دوم کمتر می‌شود و هرچه میانگین واقعی به فرض صفر نزدیک تر شود احتمال خطای نوع دوم بیشتر می‌شود. اما واقعیت این است که در بسیاری از موقعیت‌های عملی، اگر میانگین واقعی به مقدار فرض صفر نزدیک باشد، نگران خطای نوع دوم نخواهیم بود و کشف آن برای ما اهمیتی نخواهد داشت. ما بسیار علاقه مند به تشخیص تفاوت های بزرگ بین میانگین واقعی و مقدار مشخص شده در فرضیه صفر خواهیم بود.

ناحیه سایه زده شده در اشکال زیر احتمال خطای نوع دوم است. توزیع نرمال سمت چپ، توزیع آماره آزمون در صورت درست بودن فرض صفر و توزیع نرمال سمت راست، توزیع آماره آزمون به ازای درست بودن فرض یک می‌باشد. همانطور که در شکل نیز واضح است، توزیع و پراکندگی نمونه‌های حول میانگین واقعی موجب می‌شود تا نمونه‌ها در بازه پذیرش قرار بگیرند و احتمال اکتشاف اختلاف میانگین واقعی و مقدار مشخص شده در فرض صفر را پایین تر بیاورد.

 

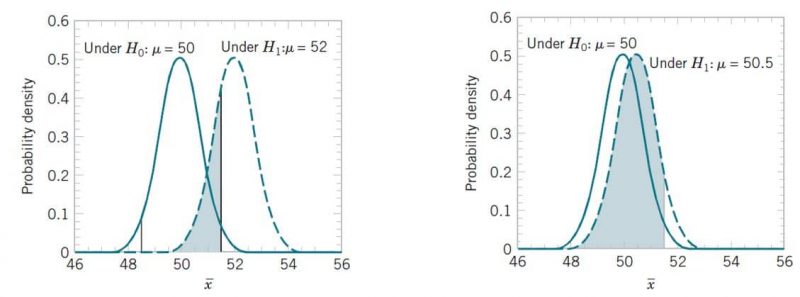
مجددا به مثال قطعات بازگردید، انحراف استاندارد طول قطعات را در شرایطی که از توزیع نرمال پیروی می‌کند ۲.۵ و اندازه نمونه را ۱۰ در نظر بگیرید. در صورتی که میانگین واقعی طول قطعات برابر ۵۲ باشد، میزان خطای نوع دوم را محاسبه کنید.

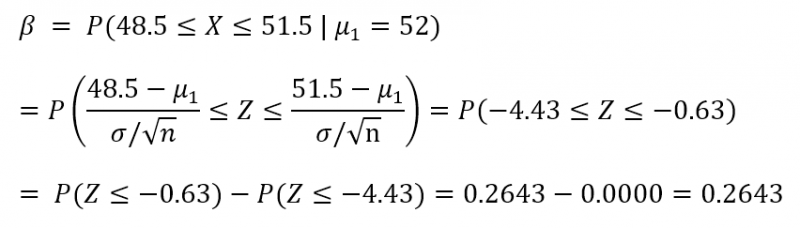
نکته: با توجه به نمودارهای بالا رابطه خطای نوع اول و خطای نوع دوم واضح است. طبیعتا در صورتی که بازه پذیرش کوچکتر شود، ناحیه بحرانی یا عدم پذیرش بزرگتر می‌گردد و خطای نوع اول افزایش می‌یابد اما از سمت دیگر نمونه‌های کمتری از توزیع واقعی در بازه پذیرش قرار می‌گیرد و این یعنی خطای نوع دوم کاهش می‌یابد.

نکته: با افزایش اندازه نمونه، احتمال خطای نوع دوم مشروط بر اینکه سطح معناداری ثابت بماند کاهش خواهد یافت.

توان آزمون:

به طور کلی، تحلیلگر زمانی که مقادیر بحرانی (در مثال قطعات ۴۸.۵ و ۵۱.۵ بودند) را انتخاب می‌کند، احتمال خطای نوع اول یا همان α را تعیین می‌کند. بنابراین، تحلیلگر به راحتی می‌تواند خطای نوع اول را مقدار دلخواهی تنظیم کند و تحت کنترل داشته باشد. از آنجایی که تحلیلگر می‌تواند مستقیماً احتمال رد کردن نادرست فرض صفر را کنترل کند، ما همیشه رد فرض صفر را به عنوان یک نتیجه گیری قوی در نظر می گیریم.

از آنجایی که احتمال خطای نوع اول تحت کنترل ماست، این سوال منطقی پیش می‌آید که چه مقداری باید استفاده شود. احتمال خطای نوع اول معیاری برای ریسک است، به عبارتی یعنی خطر و پیامدهای نتیجه گیری اینکه فرضیه صفر نادرست است در حالی که واقعاً اینطور نیست چقدر است؟ مقادیر کوچکتر α پیامدهای جدی تری را منعکس می‌کند و مقادیر بزرگتر α با پیامدهای با اهمیت کمتر را نیز شامل می‌شود. در بیشتر موقعیت‌ها استفاده از مقدار ۰.۰۵ متدوال است. در مثال قطعات تولیدی با اندازه نمونه ۱۰ تایی، مقادیر بحرانی ۴۸.۴۵ و ۵۱.۵۵ به دست خواهند آمد.

از طرف دیگر، احتمال خطای نوع دوم یا β ثابت نیست بلکه به مقدار واقعی پارامتر و اندازه نمونه‌ای که انتخاب کرده‌ایم بستگی دارد. از آنجایی که احتمال خطای نوع β تابعی از حجم نمونه و میزان نادرست بودن فرض صفر است، مرسوم است که تصمیم به پذیرش فرض صفر را یک نتیجه گیری ضعیف عنوان کنیم، مگر اینکه بدانیم β به طور قابل قبولی کوچک است. بنابراین، به جای بیان عبارت «فرض صفر را می‌پذیریم»، اصطلاح «عدم رد فرض صفر» را ترجیح می‌دهیم. عدم رد فرض صفر به این معنی است که ما شواهد کافی برای رد فرض صفر پیدا نکرده‌ایم.

یک شباهت مفید میان آزمون فرض و دادگاه هیئت منصفه وجود دارد. در محاکمه، متهم بی گناه فرض می شود (مانند فرض صفر) اما اگر شواهد محکمی بر خلاف آن یافت شود، متهم مجرم شناخته می‌شود (رد فرض صفر) در غیر این صورت اگر شواهد کافی نباشد، متهم بی گناه اعلام می‌شود. این به معنی اثبات بی‌گناهی متهم نیست و مانند عدم رد فرض صفر، نتیجه گیری ضعیفی است.

در این زمینه، مفهوم مهمی که ما از آن استفاده می‌کنیم، قدرت آزمون آماری است. قدرت یک آزمون فرض آماری احتمال رد فرض صفر در صورت درست بودن فرض یک است. توان آزمون بصورت زیر محاسبه می‌شود:

بدست آوردن احتمال خطای نوع دوم:

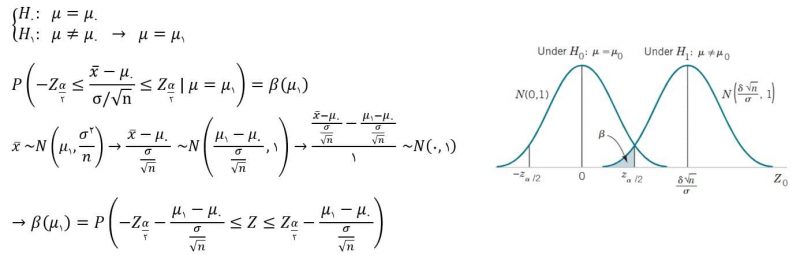
در این مرحله تقریب می‌زنیم و از حد پایین بازه صرف نظر می‌کنیم.

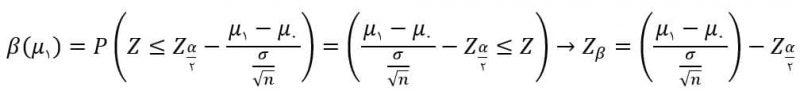
کنترل خطا و تعیین اندازه نمونه:

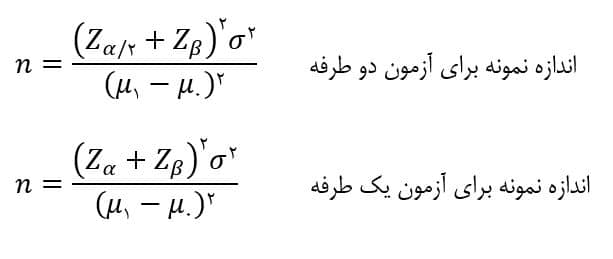
آزمون فرض یک طرفه:

در تعریف فرضیه‌ها، ما همیشه فرض صفر را بصورت یک گزاره برابری بیان می‌کنیم. اما فرض یک بسته به تصمیم ما در صورت رد فرض صفر ممکن است یک طرفه یا دو طرفه باشد. اگر هدف طرح ادعاهایی شامل عباراتی مانند بیشتر از، کمتر از، برتر از، حداقل و حداکثر باشد، آزمون فرض یک طرفه خواهد بود اما اگر هیچ جهتی در ادعا ذکر نشده باشد، یا ادعای تساوی یا عدم تساوی مطرح شود، باید از یک آزمون فرض دو طرفه استفاده شود.

توجه داشته باشید که اگرچه فرض صفر با علامت تساوی بیان می‌شود، اما درک می‌شود که شامل هر مقداری از پارامتر مورد مطالعه که توسط فرض یک مشخص نشده باشد می‌شود و به صورت ضمنی یک گزاره بزرگتر مساوی یا کوچکتر مساوی است. بنابراین، رد نکردن H_۰ به این معنا نیست که پارامتر مورد مطالعه برابر مقدار مشخص شده در فرض صفر است، بلکه تنها به این معناست که ما شواهد قوی در حمایت از H_۱ نداریم. در ادامه تمامی فرض‌های صفر بطور ضمنی بیان شده اند.

فرض سختگیرانه و سهل‌گیرانه:

در نحوه تعریف فرض یک مساله برای ترتیب یک آزمون یک طرفه، از نظر یک طرفه سمت راست یا یک طرفه سمت چپ، بحثی وجود دارد. همانطور که در بالا گفته شد، در آزمون فرض یک طرفه، رد نشدن H_۰ به این معناست که ما شواهد قوی در حمایت از H1 نداریم. مساله‌ای را فرض کنید که در آن μ پارامتری است که کمتر بودن آن مطلوب می‌باشد و سقف مجاز آن از نظر ما μ_۰ است.

در فرض سهل گیرانه، احتمالی وجود دارد که حتی اگر مقدار μ بزرگتر از μ_۰ باشد، باز هم فرض صفر رد نشود. به نمودار بالایی که مربوط به فرض سهل‌گیرانه است توجه کنید. فرض ابتدایی این است که میزان پارامتر مطلوب است، و بر این اساس مناطق ۱، ۲ و ۳ جزوی از ناحیه پذیرش اند و نتیجه آنها، رد نشدن فرض صفر و تصمیم بر مطلوب بودن میزان μ است. اما در آزمون سختگیرانه، میزان پارامتر در ابتدا نامطلوب فرض شده است و تنها ناحیه ۱ که ناحیه رد فرض صفر است، نشانگر مطلوب بودن میزان این پارامتر می‌باشد. بنابراین شانس پذیرفته شدن مطلوب بودن میزان پارامتر در آزمون سهل‌گیرانه بیشتر از سخت‌گیرانه خواهد بود و تفاوت این دو آزمون در ناحیه ۳ آزمون سهل‌گیرانه و ناحیه ۲ آزمون سختگیرانه  است که آن را منطقه ارفاق می‌نامند. این منطقه با توجه به انتخاب فرض یک، میزان پذیرش فرض صفر را افزایش می‌دهد و آزمون را به نفع فرض صفر برگزار می‌کند و از همین جهت ارفاق نامیده می‌شود. سهل‌گیرانه یا سختگیرانه بودن آزمون، نسبی است و باید مشخص شود از چه دیدی یا نسبت به چه موقعیتی بیان شده است. بطور معمول و در مسائل تامین مواد اولیه یا خرید کالا، در صورتی که تامین کننده از سابقه خوبی برخوردار نبوده یا مشخصه در حال بررسی شدیدا حیاتی باشد، فرض بصورت سختگیرانه نسبت به تامین کننده تعریف خواهد شد تا بتوان با شواهد قوی تصمیم بر تایید تامین کننده اتخاذ کرد.

بنابراین بطور خلاصه، در آزمون فرض یک طرفه، باید به خاطر داشته باشیم که رد فرض صفر همواره یک نتیجه گیری قوی است که نیاز به شواهد قوی دارد و به عبارتی آزمون به نفع فرض صفر برگزار می‌گردد. در نتیجه، باید تعریف فرض‌های ما بصورتی انجام شود که نتیجه گیری قوی در مورد آن در فرض یک لحاظ گردد. در مسائل دنیای واقعی، این اغلب به دیدگاه و تجربه‌ی ما در مورد موقعیت بستگی دارد.

روش عمومی آزمون فرض:

توصیه می‌شود روش آزمون فرض به ترتیب از مراحل زیر بکار گرفته شود:

• پارامتر مورد مطالعه

با توجه به زمینه مساله، پارامتر مورد علاقه برای بررسی شناسایی و تعیین شود.

• فرض صفر

فرض صفر بیان شود.

• فرض یک

فرض جانشین مناسبی با توجه به موقعیت بیان شود.

• آماره آزمون

یک آماره مناسب تعیین شود.

• معیار رد شدن فرض صفر

ناحیه بحرانی یا همان ناحیه رد فرض صفر در یک سطح معناداری ثابت بیان شود.

• محاسبات

مقادیر نمونه لازم محاسبه شده و در معادله آماره آزمون قرار داده شده و مقدار آن محاسبه شود.

• نتیجه گیری (قضاوت)

درباره رد شدن یا نشدن فرض صفر تصمیم گیری شود و تفسیر آن در زمینه مساله گزارش شود.