مقالات آمار و احتمال
آزمون فرض و فاصله اطمینان برای مقایسهی واریانس دو توزیع نرمال
ویدوی آموزشی
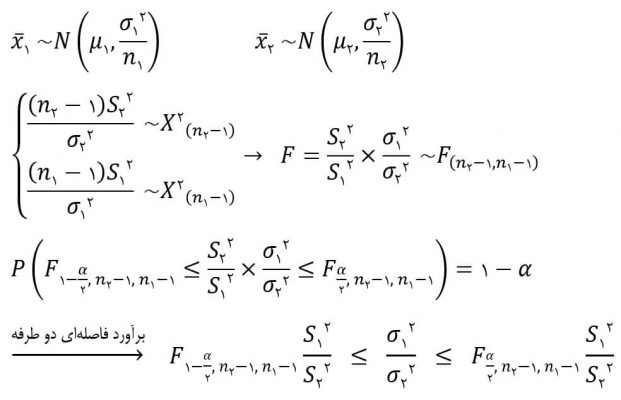
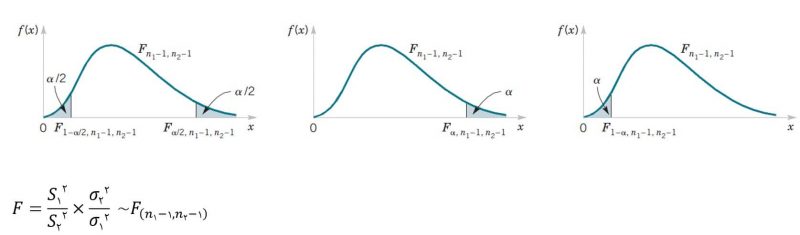
متغیر تصادفی F دارای دو پارامتر مجهول σ۱۲ و σ۲۲ است. برای ترتیب دادن آزمون فرض، به آماره نیاز داریم و در اینجا برای بدست آوردن آماره، با توجه به فرض صفر، نسبت δ۲=σ۲۲ /σ۱۲ را مقداردهی میکنیم که در آزمون برابری واریانس دو جامعه، این مقدار برابر یک خواهد بود.
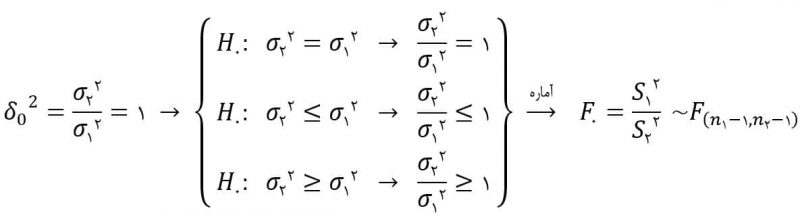
نکته: در آزمون فرض برابری میانگین دو جامعه، تفاوت میانگین دو جامعه با صفر مقداردهی میشد. Δ۰=μ۱-μ۲=۰
اما در آزمون فرض برابری واریانس دو جامعه، نسبت واریانس دو جامعه با یک مقداردهی میشود. ۱=δ۲=σ۲۲ /σ۱۲
Table of Contents
استفاده از برآورد فاصلهای به جای آزمون فرض در حالت دو پارامتری:
در مقایسهی واریانسها، ابتدا بازه برآورد فاصلهای را برای پارامتر مورد مطالعه یعنی σ۲۲ /σ۱۲ بدست میآوریم:
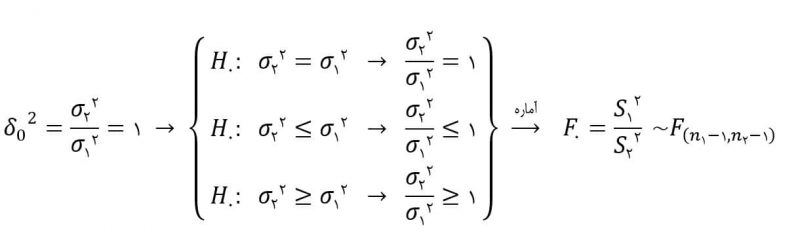
بر اساس حالتهای زیر تصمیمگیری میکنیم:

بطور مشابه، در مقایسه میانگینها باید قرار داشتن مقدار Δ۰ در بازه برآورد فاصلهای برای Δ را بررسی کرد. در صورتی که آزمون بر روی مقایسه میانگینها باشد، این مقدار برابر Δ۰=۰ خواهد بود.
مثال. ضخامت لایه اکسید یک عایق برای عملکرد مناسب یک عایق موضوع مناسبی میباشد. بر این اساس تغییرات ضخامت به عنوان یک فاکتور کلیدی مورد توجه بوده و تغییر پذیری پایین برای انجام فرآیندهای بعدی مطلوب میباشد. دو ترکیب مختلف مورد مطالعه قرار گرفته تا ببینیم کدام یک از آنها در کاهش میزان تغییرات ضخامت لایه اکسید موفقتر عمل میکند. به این منظور دو نمونه مجزای ۱۶ تایی گرفته شده است و S۱=۱.۹۶ و S۲=۲.۱۳ میباشد. آیا شواهدی دال بر برتری هر یک از ترکیبهای مورد استفاده مشاهده مینمایید؟ آلفا ۰.۰۵
پاسخ:
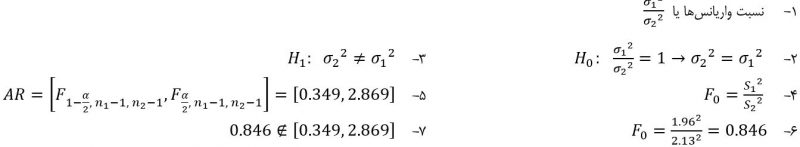
فرض صفر قبول میشود که در تفسیر یعنی شواهدی بر اینکه تفاوتی بین دو ترکیب وجود دارد یافت نشد.
خطای نوع دوم و تعیین اندازه نمونه:
ابتدا پارامتر λ=σ۱/σ۲ را بدست میآوریم و سپس با استفاده از منحنی OC مربوط به توزیع F دو طرفه یا یک طرفه و سطح معناداری معین، در کنار پارامترهای β و n به شیوه قبلی عمل میکنیم.
